что такое аффинное преобразование

Что за зверь — аффинные преобразования?

Скорее всего, каждый из Вас хоть раз в жизни слышал термин «аффинные преобразования». Действительно, все постоянно о них говорят: «инвариантность к аффинным преобразованиям», «аугментация с помощью аффинных преобразований», «аффинные преобразования в компьютерной графике» и так далее. Однако, далеко не все могут сходу ответить на простой вопрос: «А расскажите, что такое аффинные преобразования простыми словами».

Вы сможете? В любом случае, давайте немного обсудим этот вопрос.

Что такое аффинное преобразование?

Аффинное преобразование (от лат. affinis «соприкасающийся, близкий, смежный») — отображение плоскости или пространства в себя, при котором параллельные прямые переходят в параллельные прямые, пересекающиеся — в пересекающиеся, скрещивающиеся — в скрещивающиеся.

Внесем немного ясности.

Во-первых, что значит «отображение в себя»? Это значит, что если мы находились в пространстве , то после образования мы должны остаться в нем же. Например: если мы применили какое-то преобразование к прямоугольнику и получили параллелепипед, то мы вышли из в . А вот если из прямоугольника у нас получился другой прямоугольник, то все хорошо, мы отобразили исходное пространство в себя. Формально это описывается так: «преобразование отображает пространство в ». Если записать с помощью формул: .

В целом, это определение уже нам что-то говорит и мы начинаем потихоньку рисовать для себя картинку. Как минимум, мы должны остаться в той же плоскости: значит мы представляем себе декартову систему координат. Здесь речь идет о нескольких прямых, так что давайте представим 2 параллельных линии. Из определения мы понимаем, что после преобразования эти линии должны остаться параллельными. Ну что ж, тогда просто сдвигаем их куда-нибудь из исходного местоположения, да и все.

Но давайте пойдем чуть дальше и дадим еще одно определение (не нами придуманное).

Преобразование плоскости называется аффинным, если оно непрерывно, взаимно однозначно и образом любой прямой является прямая.

Звучит это, пожалуй, чуть сложней и путанней, но дает нам больше конкретной информации, чем предыдущее определение.

Итак, с определениями мы разобрались. Давайте теперь запишем в общем виде, а как выглядит преобразование координат в формульном виде.

При этом, числа должны образовывать невырожденную матрицу:

На всякий случай: матрица называется невырожденной, если ее определитель не равен нулю, т.е.

Можно записать и в более общем в виде.

Аффинное преобразование — преобразование вида , где — обратимая матрица, а . В данном случае, само собой, -мерный вектор.

Примеры аффинных преобразований

Мы с Вами достаточно подробно разобрали, что такое аффинное преобразование и как его можно описать с помощью формул. Давайте теперь рассмотрим популярные примеры.

Приходят ли Вам в голову какие-нибудь претенденты на роль? Позвольте мы внесем свои предложения.

Поворот

Пусть .

Значит, матрица примет вид:

И новые координаты будут выглядеть так:

Растяжение-сжатие

Теперь мы предлагаем сконструировать матрицу несколько иначе:

Новые координаты тогда принимают вид:

В целом, тут даже уже из вида системы уравнений понятно, что мы просто растягиваем наши оси, если коэффициент меньше 1 и сжимаем, если больше 1. Пример на рисунке.

Сдвиг

Ну и давайте напоследок еще один пример.

Пусть теперь матрица никак не меняет исходные координаты (т.е. ). А вот пусть равняется , а .

Таким образом, наша система принимает вид:

Если отразить это на графике, то мы просто сдвинули начало координат в точку . Вот, собственно, и вся премудрость.

Эпилог

Источник

Аффинные преобразования

Содержание

Определение аффинных преобразований [ править ]

Давайте поговорим о растяжениях и сжатиях плоских фигур.

Если растянуть вдоль какого-то направления круг, то получится лекальная кривая — эллипс.

Если растянуть квадрат в направлении, параллельном одной паре сторон, то получится прямоугольник. Если же квадрат растянуть или сжать в направлении его диагонали, то получится параллелограмм.

Но что такое растяжение и сжатие? Как их строго определить?

Растяжения и сжатия, о которых мы будем говорить, в определенном смысле, равномерные.

Эта равномерность означает, что все кусочки плоскости будут растягиваться (сжиматься) одинаково.

Кроме того, когда мы растягиваем (сжимаем) квадрат, его стороны — отрезки остаются отрезками.

Такие равномерные растяжения (сжатия) называются аффинными преобразованиями.

Преобразование плоскости называется аффинным, если оно взаимно однозначно и образом любой прямой является прямая. Преобразование называется взаимно однозначным, если оно разные точки переводит в разные, и в каждую точку переходит какая-то точка.

Напомним, что преобразование — это отображение множества на само себя. Отображение называется взаимооднозначным (биективным), если разные элементы переходят в разные, и в каждый элемент, какой-то элемент переходит.

Частным случаем аффинных преобразований являются просто движения (без какого-либо сжатия или растяжения). Движения — это такие преобразования, которые сохраняют расстояние между любыми двумя точками неизменным, а именно параллельные переносы, повороты, различные симметрии и их комбинации.

Другой важный случай аффинных преобразований — это растяжения и сжатия относительно прямой.

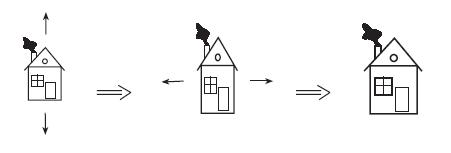
На рисунке 1 показаны различные движения плоскости с нарисованным на ней домиком. А на рисунке 2 показаны различные аффинные преобразования этой плоскости.

Рисунок 1. Примеры движений.

Рисунок 2. Примеры аффинных преобразований.

Множество движений есть подмножество множества аффинных преобразований.

Это кажется очевидным. Давайте поймем, что нам собственно нужно доказать. Для этого нужно ещё раз посмотреть на определения движения и аффинных преобразований. Нужно доказать, что любое движение является аффинным. То есть нужно показать, что при движении разные точки переходят в разные, и образ любой прямой есть прямая.

Это интуитивно ясно — при движении фигуры вообще не меняют своей формы и размеров, а меняют лишь своё положение на плоскости. Также и прямые будут сохранять свою форму — оставаться прямыми. Движение можно представлять как перемещение листка бумаги с рисунком по парте. При движении разные точки остаются разными, поскольку расстояния сохраняются. Если точки были «разделены» некоторым расстоянием, то и после движения они будут «разделены» этим же расстоянием.

Растяжения и сжатия [ править ]

Рисунок 3. Сжатия и растяжения относительно прямой.

Давайте докажем, что растяжение (сжатие) относительно прямой является аффинным преобразованием. Во-первых, эти преобразование взаимно однозначно. Чтобы доказать это заметим, что для каждого сжатия есть растяжение, которое все точки возвращает на свои места, и наоборот, для каждого растяжения есть возвращающее всё на свои места сжатие. А сейчас воспользуемся теоремой:

Растяжение (сжатие) относительно прямой есть аффинное преобразования.

Итак, кроме движений плоскости аффинные преобразования содержат еще сжатия и растяжения относительно прямой. Если мы применим растяжение относительно одной прямой, а потом относительно другой прямой, то снова получим аффинное преобразование, так как и первое, и второе растяжение сохраняло прямые и разные точки переводило в разные. Вообще верно

Композиция аффинных преобразований есть снова аффинное преобразование:

Рисунок 4. При параллельном проектировании с одной плоскости на другую фигура подвергается растяжению (сжатию) относительно прямой пересечения плоскостей.

Докажите, что при параллельной проекции фигуры с одной плоскости на другую, фигура на второй
1) совпадает с тем, что изображено на первой, если плоскости параллельны;
2) является растяжением (сжатием) того, что изображено на первой плоскости, относительно прямой пересечения плоскостей, если плоскости пересекаются.

Гомотетия [ править ]

Есть еще важный класс аффинных преобразований — это сжатия и растяжения относительно точки. Они называются преобразованиями подобия или гомотетиями.

Что такое гомотетия с коэффициентом

а) Тождественное преобразование (преобразование, которое ничего не преобразует, а все оставляет на своих местах);

Как вы узнали из задачи 2(ссылка), растяжение (сжатие) относительно прямой можно реализовать как проекцию фигуры с помощью параллельного пучка лучей с одной плоскости на другую плоскость, не параллельную ей. А гомотетия получается при проекции с помощью центрального пучка лучей с одной плоскости на другую, параллельную ей плоскость (рис.5).

Какое преобразование обратно гомотетии с коэффициентом

Рисунок 5. Гомотетия как проекция фигуры с одной плоскости на другую, параллельную ей плоскость с помощью центрального пучка лучей.

Мы уже выяснили, что

Докажите, что гомотетия относительно точки тоже аффинное преобразование:

Подсказка Это можно сделать, решив следующую задачу. Кроме того, есть простой путь для тех, кто освоился с декартовой системой координат. Поместите начало системы координат в центр гомотетии и определите, что происходит при гомотетии с координатами точки. Как выглядит общее уравнение прямой? Почему прямые при гомотетии остаются прямыми?

Подсказка Смотрите рисунок 6.

Рисунок 6. Из двух растяжений вдоль перпендикулярных направлений получается гомотетия.

Докажите, что при гомотетии все расстояния увеличиваются (уменьшаются)

Докажите, что при гомотетии окружности переходят в окружности, а правильные треугольники — в правильные треугольники.

Докажите, что композиция двух гомотетий есть снова гомотетия, причем центры всех трех гомотетий лежат на одной прямой.

Что аффинные преобразования сохраняют? [ править ]

Из определения аффинных преобразований видно, что они сохраняют прямые и свойство различия двух точек:

Эти два свойства можно обозначить так:

Эти два свойства являются определяющими свойствами аффинных преобразований. Непосредственно из этих свойств следуют, как мы уже показали ранее, следующие два важных свойства

Эти свойства можно обозначить так:

Следующие свойства относятся к классу «законов сохранения», то есть они говорят, какие свойства фигур аффинные преобразования сохраняют (не изменяют).

Примечание Преобразование инверсии сохраняет свойство окружности и углы между кривыми. Другой тип преобразований — движения, они сохраняют расстояния. Движения, аффинные преобразования и инверсию можно грубо определить так:

Докажите, что при аффинном преобразовании

Эти свойства можно обозначить так:

Задача 12[9] На основе предыдущих свойств, докажите следующие два свойства:

Рисунок 7. Отношение площадей сохраняется.

Следующее важное свойство касается площади. Посмотрите на рисунок 7. Там нарисована прямоугольная сетка и две фигуры. Площади этих фигур примерно равны (пропорциональна) количеству квадратиков. А отношение площадей двух фигур примерно равно отношению квадратиков внутри этих фигур.

При аффинном преобразовании квадратики переходят в одинаковые параллелограммы, прямоугольная сетка переходит в скособоченную сетку. Но важно, что отношение площадей примерно равно отношению числа этих параллелограммчиков, то есть тому же, чему было равно это отношение до аффинного преобразования. Если нарисовать сетку очень-очень мелкой, точнее сколь угодно мелкой, тогда площадь будет точно выражаться через число квадратиков и параллелограммчиков и наши рассуждения станут строгими.

Таким образом, мы доказали еще одно свойство:

S F 1 : S F 2 = S F ′ 1 : S F ′ 2 <\displaystyle S_>\,:\,S_>=S_<_<1>>\,:\,S_<_<2>>\,\!>

Это свойство можно записать так:

Рисунок 8. Отношение длин отрезков на прямой сохраняется.

Докажите, что отношение длин отрезков на одной и то же прямой при аффинном преобразовании сохраняется.

Заметьте, что любое действительное число можно сколь угодно точно приблизить рациональным числом. Это свойство математики обозначают так: «множество рациональных чисел всюду плотно». В сколь угодно маленькой окрестности любого числа найдется рациональное число.

Докажите, что отношение длин отрезков на параллельных прямых при аффинном преобразовании сохраняется:

Подсказка Используйте подсказку к предыдущей задаче.

При строгом доказательстве свойств 9 ∘ <\displaystyle 9^<\circ >\,\!> и 10 ∘ <\displaystyle 10^<\circ >\,\!> используется предельный переход и свойство непрерывности аффинных преобразований. Про непрерывность и предельные переходы рассказывают на на первом курсе института. Мы с вами использовали предельный переход на интуитивном уровне.

Докажите, что при аффинном преобразовании выпуклой фигуры получается выпуклая фигура. Фигура называется выпуклой, если любыми двумя точками она содержит и отрезок, их соединяющий. Другими словами, аффинные преобразования сохраняют свойство выпуклости.

Что могут аффинные преобразования? [ править ]

Итак, мы выяснили, что сохраняют аффинные преобразования. Теперь посмотрим, на что они способны. Можно ли с помощью аффинного преобразования из трапеции сделать квадрат? Или из параллелограмма — квадрат? Из любого ли треугольника можно сделать правильный треугольник? Постараемся выяснить, какими деформирующими способностями обладают аффинные преобразования.

Основываясь на рисунке 9, решите следующие задачи.

Покажите, что с помощью сжатия(растяжения) относительно одной из сторон из любого треугольника можно сделать равнобедренный.

Покажите, что с помощью сжатия(растяжения) относительно основания из равнобедренного треугольника можно сделать правильный.

Покажите, что с помощью гомотетии относительно центра правильного треугольника из него можно получить правильный треугольник с единичной стороной.

Рисунок 9. Превращение треугольника в правильный.

Докажите, что не из всякого четырехугольника можно сделать квадрат.

Решение. Возьмите четырехугольник с непараллельными сторонами. Они останутся непараллельными.

Докажите, что не из всякого пятиугольника (шестиугольника) можно сделать правильный пятиугольник(шестиугольник).

Докажите, что из круга нельзя сделать квадрат, а из квадрата нельзя сделать треугольник.

Каждая диагональ выпуклого пятиугольника параллельна одной из его сторон. Докажите, что аффинным преобразованием этот пятиугольник можно

Эллипс — это фигура на плоскости, которая в подходящих декартовых координатах задается уравнением

Эллипс — это фигура, которую можно получить из круга, применяя аффинное преобразование.

Докажите, что эти два определения эллипса равносильны.

Подсказка Эта задача включает в себя две задачи. Сначала нужно показать, что из первого определения следует утверждение второго определения, потом наоборот. Вторая часть сложнее, так как для неё необходимо иметь представление о всех возможных аффинных преобразованиях.

Докажите, что применяя движения, растяжения и сжатия относительно прямых, можно получить любое аффинное преобразование.

Подсказка Решите сначала следующие три задачи.

Докажите, что если аффинное преобразование сохраняет неподвижными все точки на двух пересекающихся прямых, то это преобразование все остальные точки плоскости тоже оставляет неподвижными.

Докажите, что из любой трапеции афинными преобразованиями можно сделать равнобокую трапецию.

Докажите, что из любого прямоугольника можно сделать квадрат.

Докажите, что из любого треугольника можно сделать прямоугольный треугольник.

Докажите, что из любого параллелограмма можно сделать квадрат.

Парабола — это фигура, которая в подходящих координатах имеет уравнение

Докажите, что множество всех парабол — это множество всех фигур, которые можно получить из параболы y = x 2 <\displaystyle y=x^<2>\,\!> при помощи аффинных преобразований.

Гипербола — это фигура, которая в подходящих координатах имеет уравнение

Методы решения задач с помощью аффинных преобразований [ править ]

Докажите, что медианы треугольника пересекаются в одной точке.

Из любого треугольника можно сделать равносторонний. Давайте сделаем. Заметим, что середины сторон перешли в середины сторон и медианы перешли в медианы. В равностороннем треугольнике медианы пересекаются в одной точке в силу симметрии. Значит, в исходном треугольнике они тоже пересекались в одной точке.

Попробуйте обобщить результат задачи 36 на случай не обязательно медиан и не обязательно треугольников.

Следующая задача решается аналогичным образом.

Обычно, задачу можно решить методом аффинных преобразований, если нужно найти отношение длин, или отношение площадей, или доказать параллельность. Причем в условии задачи не должно быть дано ничего такого, что не сохраняется при аффинных преобразованиях. Например, если в задаче дано точное значение какого-то угла, то, скорее всего, эта задача не решается методом аффинных преобразований.

Через каждую вершину треугольника проведены две прямые, делящие противоположную сторону треугольника на три равные части. Докажите, что диагонали, соединяющие противоположные вершины шестиугольника, образованного этими прямыми, пересекаются в одной точке.

Источник

Аффинные преобразования на плоскости

IP76 > Аффинные преобразования на плоскости

В интернете полно теории по аффинным преобразованиям. Повторяться смысла нет. Теоремы, доказательства, утверждения — это безусловно интересно, но сайт заточен на практическое применение. Поэтому больше интересует метод, а не теория.

В основе метода лежит изменение единичной матрицы с учетом матриц масштабирования, перемещения, сдвига и поворота. Эти матрицы являются справочными и также легко находятся в интернете.

Не смотря на простоту метода, с его применением возникают какие-то сложности, связанные, видимо, с непониманием, почему именно такие матрицы, почему важен порядок, почему это должно работать.

Хотя, как мне кажется, больше отпугивает само понятие матрицы. Давайте немного поботаним.

Поворот

Предположим, стоит задача повернуть прямоугольник на некоторый угол относительно его центра. Очевидно, надо рассчитать 4 угловые точки и построить по ним полигон.

Рис.1. Поворот точки Р1 на угол β

Имеем некий прямоугольник с вершинами в точках P1, P2, P3, P4. Рассмотрим точку P1(x,y). Она отстоит от оси абсцисс на угол α. Повернем ее на угол β. Очевидно, что вращение происходит по окружности с центром, находящимся в центре заданного прямоугольника O(x,y).

Рассчитаем координаты новой точки P1′( x′, y′).

Где R – радиус окружности на которой расположена точка P1, и равен (O, P1). Воспользуемся формулами сложения углов (1.1 и 2.1) из справочника:

Рис.2. Координаты точки P1 через угол α

Замечаем, что R × cos(α) это не что иное, как координата X точки P1, а R × sin(α) – координата Y. Таким образом, формулы расчета координат новой точки P1′ приобретают вид:

Чтобы выйти на правильную позицию на холсте, прибавим к полученным значениям координаты центра прямоугольника:

И мы только что получили матрицу поворота аффинного преобразования.

Рис.3. Поворот прямоугольника на угол β относительно его центра

В общем виде формулы можно записать как:

Где: M11, M12, M21, M22, Dx, Dy – коэффициенты, определяющие преобразование.

Теперь представим себе, что прямоугольник – это на самом деле бесконечная плоскость. И к каждой точке этой плоскости применены одна и те же формула трансформации. Вот это и будет называться аффинным преобразованием на плоскости.

Таким образом, матрицей поворота будет следующая:

Сдвиг

Еще одно интересное преобразование. Состоит из вертикального сдвига, когда меняется только координата Y, и горизонтального, когда меняется только X.

Для определения величин сдвигов будем использовать углы отклонения от горизонтали или вертикали, т.к. это наиболее часто встречающаяся ситуация.

Снова рассматриваем прямоугольник, помня, что это на самом деле плоскость.

Рис.4. Плоскость с центром трансформации в левой нижней точке P3

Для наглядности деформация будет происходить относительно левой нижней точки P3.

Вначале деформируем следующим образом:

Рис.5. Вертикальный сдвиг

При вертикальном сдвиге координаты X не меняются. Изменяются координаты Y. В данном случае координата Y точки P1 изменилась на расстояние (P2,P2′).

Из чего получим формулу преобразования для Y:

Рис.6. Вертикальный + горизонтальный сдвиги

Теперь добавим горизонтальный сдвиг. Координата X точки P1 изменилась на расстояние (P4,P4′), которое рассчитывается аналогичным образом.

В итоге, формулы для трансформации сдвига выглядят следующим образом:

В позиции M12 находится коэффициент, на который нужно умножить расстояние X, чтобы получить величину вертикального смещения по Y. Аналогично, в позиции М21 находится коэффициент, на который умножается расстояние Y для определения горизонтального сдвига. Это на тот случай, если не нужны углы и заранее знаем, на какие величины хотим деформировать.

Перемещение и масштабирование

Это очень простые матрицы и в свете всего вышесказанного, думаю, понятные и останавливаться на них особого смысла нет. Поэтому, для полноты картины, просто приведу.

Композиция

Сразу извинюсь перед хранителями традиций. Композиция, строго говоря, не перемножение матриц, хотя бы потому, что производится в порядке, обратном стандартному перемножению. Но давайте будем честными, как ни назови, и в каком порядке производится — это умножение матриц. И у нас это будет стандартно — слева направо.

Предположим, у нас есть следующее преобразование:

На которое следом идет такое преобразование:

Раскроем скобки и преобразуем:

Это ничто иное, как перемножение матриц коэффициентов:

Соответственно, расчет новых координат выглядит как:

Понятно, что можно умножить получившуюся матрицу на матрицу третьего преобразования, четвертого и т.д. Таким образом, чтобы получить коэффициенты сложного аффинного преобразования, нужно перемножить матрицы коэффициентов в порядке применения трансформаций.

Утверждение, прямо скажем, смелое, но правильное.

Проверим. Допустим, я хочу вначале применить деформацию, а потом повернуть на угол.

Рис.7. Деформация без поворота

На рисунке 7 пока только деформация. Теперь к деформированному прямоугольнику (плоскости) применяю поворот на 80 градусов.

Рис.8. Деформация + поворот

Расчет координат в точности воспроизводит приведенные выше выкладки:

Применение

Аффинные преобразования изменяют геометрию плоскости, при этом сохраняя параллельность линий и соотношение расстояний.

Безусловно, это один из основных методов обработки изображений. Аффинные преобразования используются для исправления искажений и деформаций, возникающих при не самых идеальных ракурсах камеры. Широко используется в машинном обучении и компьютерном зрении.

Лично мне чаще всего попадались проблемы, которые обобщенно можно выразить двумя вопросами:

Эти два вопроса объединяет одно. Изображение – набор точек, эллипс — геометрическое место точек. Решая вопрос в лоб, надо к каждой точке применить функции поворота. И если для изображения – ну, может быть, то к эллипсу, как фигуре векторной графики, это выглядит топорней некуда.

Аффинное преобразование – это преобразование плоскости. Применяя к плоскости некую трансформацию, мы понимаем, что эта трансформация применяется к каждой точке плоскости. Чтобы плоскость не содержала, это вытянется, сожмется, деформируется, повернется вместе с плоскостью.

Центр трансформации

Все что мы делали ранее, происходило относительно либо центра прямоугольника, либо одной из его вершин. Это центр трансформации. По сути – это начало координат той координатной системы, в которой происходит трансформация. Поэтому, перед всеми преобразованиями необходимо установить центр системы координат.

В Windows этим занимается функция:

С этой функцией обычно идет еще набор функций, типа изменения окна вывода. Сейчас пока это все не нужно. После применения этой функции начало координат из верхнего левого угла переместиться в указанную точку. Все геометрические построения должны это учитывать. Поэтому лучше изначально писать код так, чтобы все рисовки были в относительных координатах.

Аффинное преобразование Windows

В основе работы с аффинным преобразованием лежит изменение матрицы с учетом масштабирования, перемещения, деформации или поворота. В Windows GDI за матрицу отвечает класс TXForm.

Знакомые обозначения. Поля имеют смысл ровно тот, который описан и в справочнике, и выше в статье. Это коэффициенты матрицы преобразования.

Необходимо проинициализировать поля записи и применить преобразование функцией Windows GDI:

Однако, работать с мировыми координатами и аффинными преобразованиями в Windows GDI — удовольствие так себе. Поэтому рекомендуется это делать в GDI+.

В GDI+ есть масса вариантов, сильно облегчающих жизнь при трансформации плоскости. Но сейчас в плане статьи стоит задача работать именно через матрицы преобразования, поэтому работаем следующим образом.

Необходимо создать экземпляр класса TGPMatrix. Затем проинициализировать его методом:

Снова знакомые имена аргументов. Аргументы имеют тот же смысл, что и поля записи TXForm.

После инициализации применяем трансформацию методом TGPGraphics:

После этих манипуляций рисуем все, что хотим нарисовать, не заботясь о расчетах, углах и синусах.

Представим, что один человек рисует портрет, а второй стоит сбоку и смотрит на холст. Для него портрет выглядит деформированным, а для художника, который смотрит прямо, портрет вполне себе правильный, не трансформированный и пока нравится. Что-то похожее происходит при аффинных преобразованиях. Правда, в приведенном примере трансформация перспективная. Но сути дела это не меняет.

Рекомендован следующий порядок при работе с аффинными преобразованиями:

Композиция

Как выше говорилось, при сложном преобразовании, состоящим из нескольких трансформаций, необходимо перемножить матрицы в порядке применения преобразований. За это отвечает функция Windows GDI:

Здесь p2 и p3 — первая и вторая структуры TXForm, результат их комбинирования будет находиться в параметре p1. Т.е. надо понимать, что p3 – это преобразование, накладываемое на p2, т.е. идущее следом за ним. Порядок применения матриц очень важен.

Практика

Весь исходный код можно скачать по ссылке ниже. Чтобы не загромождать буду фрагментировать. Если приводить весь код в статье, до конца можно никогда не добраться.

Перед вызовом этой функции точка начала координат уже установлена в центр прямоугольника.

Аффинный поворот

Рис.9. «Спокойное» аффинное преобразование

Ну, это мы уже видели. Однако, если повернуть прямоугольник, за вершину P1 или в поле «Rotate Angle» увидим интересное изменение:

Рис.10. Подписи к вершинам тоже под углом

Помимо поворота непосредственно прямоугольника, повернулись и подписи вершин.

Преобразование применятся к плоскости, к каждой точке плоскости. Грубо говоря, преобразование применяется ко всему, что на плоскости.

Поэтому, можно предположить, что такой же фокус пройдет и с эллипсом:

Рис.11. Эллипс под углом

То же самое касается и изображения:

Рис.12. Изображение под углом

В чем, собственно, прелесть аффинных преобразований и состоит. Не надо считать каждую точку, писать километры кода. Мы просто рисуем, как будто и нет никаких преобразований, все также прямоугольно, параллельно и перпендикулярно. Все расчеты берет на себя плоскость, к которой применили преобразование.

Фрагмент из вышеприведенного кода:

В функции DrawEllipse нет ничего особенного, вынесена, чтобы не загромождать код:

Т.е. не взирая на все требуемые повороты, деформации и прочие издевательства, спокойно рисуем все в том же прямоугольнике val, все теми же обычными методами.

Аффинный сдвиг

Аналогичные чудеса в режиме деформации сдвига (кнопка 10):

Рис.13. Поперечная деформация (сдвиг) кота

Перед рисованием инициализируем матрицы TXForm и в зависимости, от того что требуется, применяем ту или иную матрицу. Фрагмент из кода выше:

Аффинная композиция

В коде выше присутствует композиция матриц — CombineTransform. Последовательность преобразований такая — вначале деформация, потом поворот. Проинспектируем кнопкой 11.

Рис.14. Деформированный, повернутый, замученный кот

Сравним с деформацией на рис.8. Там мы делали композицию матриц руками (в интерфейсе – режим 8), теперь этим занимается Windows GDI.

Рис.15. Все правильно делаем

Перед вызовом функции DrawAffine, необходимо перевести центр системы координат в центр прямоугольника. Напомню, начало системы координат – это центр трансформации. Именно вокруг него вертится вселенная.

Если б мышь знала… Координаты вершин

В приложении есть возможность таскать за некоторые вершины. Тут возникает проблема. Если применяем аффинное преобразование, координаты точек, за которые можно «ухватиться» сильно отличаются от координат в «нормальном» состоянии координатной системы. Поэтому, перед тем как плоскость начнет изменяться, необходимо рассчитать нужные точки, т.е. координаты, понятные мышке.

И только после этого

Функции расчета достались в наследство от предыдущих этапов, когда экспериментировали над прямоугольником без применения аффинных преобразования. Не зря ж в конечном счете экспериментировали.

Конечно, можно сформировать и скомбинировать матрицы, взять коэффициенты и посчитать по формуле. Почти как в CalcComboPoints.

В GDI+ в TGPMatrix для этих целей существуют методы:

Здесь они не используются. Потом как-нибудь обязательно вернемся к ним.

Смещать ли начало координат?

Теоретически рекомендуется делать именно так, смещать и потом трансформировать. И, возможно, это правильно. Но можно обойтись и без этого. Просто привычней работать в «обычной» системе координат, когда точка (0,0) системы находится в левом верхнем углу.

По сути, как это делается, мы уже рассмотрели в самом начале статьи, когда вращали прямоугольник, считали координаты вершин и смещали в нужное место. Давайте это сделаем с помощью аффинных преобразований.

Порядок действий таков:

Сильно сократил код за счет того, что не использую TXForm, а инициализирую сразу TGPMatrix. Что тут изменилось. В матрицу поворота добавил еще смещение в точку (ACenter.x, ACenter.y) – центр прямоугольника, или центр трансформации. Перед рисованием сместил прямоугольник отрисовки так, чтобы он оказался центрирован по началу координат, т.е. точки (0,0). Аффинное преобразование отработает поворот и сместиться на указанные величины по x и y.

Т.е. произойдет ровно тоже самое, что мы делали руками, когда прибавляли координаты центра к расчетным значениям вершин.

В демонстрационном примере это режимы 12..14, которые визуально будут совпадать с 9..11, с той лишь разницей, что перевода центра координат не происходит.

Чтобы продемонстрировать, работоспособность метода, существует последний режим – 15. Помимо основного прямоугольника, рисуется звезда и текст под углом, обратным текущему. Текст в дополнение к повороту также подвергается масштабированию.

Рис.16. Аффинные преобразования в любой требуемой точке плоскости

Я грозился вернуться к теме поворота звезд. Говорил, что есть более правильные методы. Брутальная звезда имени Стетхама, помните? Так вот, наиболее правильным будет вращать звезды, и не только, через аффинное преобразование.

Процедура, отвечающая за рисовку всего этого хозяйства:

Источник