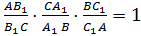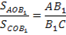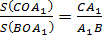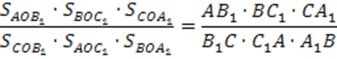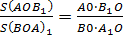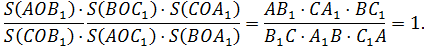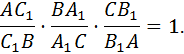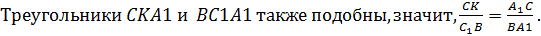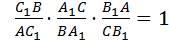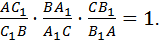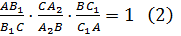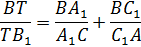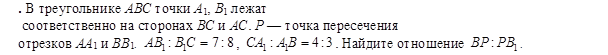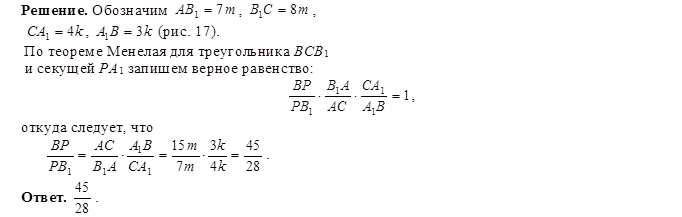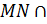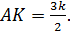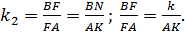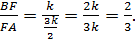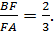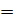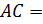Чевиана что это такое

Значение слова «чевиана»

чевиана

1. отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой на противоположной ей стороне или на её продолжении ◆ Ясно, что чевиана имеет меньшую длину, чем большая из двух сторон, выходящих из той вершины, из которой она проведена. Росс Хонсбергер, «Математические изюминки», 2008 г.

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова скоморох (существительное):

Понятия со словом «чевиана»

Отправить комментарий

Карта слов и выражений русского языка

Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.

Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.

Сайт оснащён мощной системой поиска с поддержкой русской морфологии.

Источник

Чевиана что это такое

Нередко учащиеся 9 и 11 классов сталкиваются с трудностями при решении практических задач на экзамене по математике. Это вторая часть ОГЭ/ЕГЭ, которая является наиболее сложной, и, соответственно, за которую можно набрать хорошее число баллов. Знание теорем Чевы и Менелая может значительно упростить решение таких задач.

Помимо экзаменов, изучение данной темы может помочь на олимпиадах, вступительных испытаниях и просто для погружения в удивительный математический мир.

Объект исследования: геометрические задачи, требующие нахождения отношений длин отрезков, площадей фигур.

Гипотеза: применение теорем Чевы и Менелая при решении многих задач рациональнее, чем другие способы решения.

Цель работы: Доказать теоремы Чевы и Менелая, выяснить, насколько их применение упрощает решение задач на отношение отрезков и площадей фигур.

· Рассмотреть доказательство теорем Чевы и Менелая

· Решить несколько задач с их помощью и другими способами. Выяснить какой из методов рациональнее в каждом конкретном случае

· Создать банк задач, при решении которых применение теорем Чевы и Менелая предпочтительнее.

Результатом исследования является презентация, которая поможет выпускникам 9 и 11 классов познакомится с методом решения задач на нахождение отношений длин отрезков и площадей фигур с помощью теорем Чевы и Менелая.

2.1.1 Кто такой Чева? Джованни Чева (1648-1734 г.)- итальянский инженер и математик. Основной заслугой Чевы является построение учения о секущих, которое положило начало новой – синтетической геометрии; оно изложено в сочинении «О взаимнопересекающихся прямых»(1678).

2.1.2 Что такое чевиана? Определение. Чевианой треугольника называется отрезок, соединяющий вершину треугольника с произвольной точкой противолежащей стороны, или ее продолжения.

1.1.3 Теорема Чевы
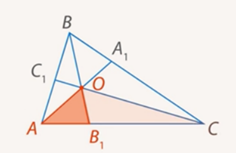
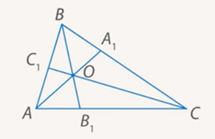
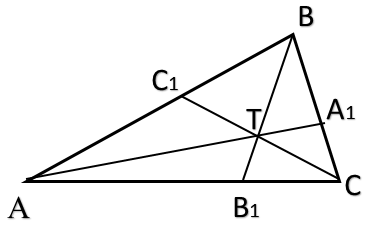
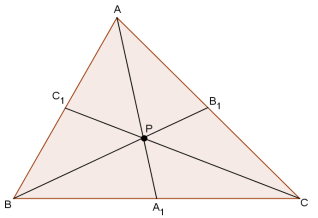
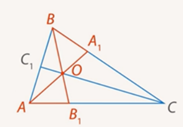
Если на сторонах AB, BC и AC треугольника ABC взяты соответственно точки C1, A1 и B1, то отрезки AA1, BB1 и CC1 пересекаются в одной точке тогда и только тогда, когда:

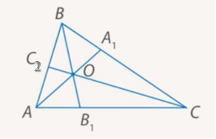
Рассмотрим треугольники AOB1 и COB1

Поскольку их основания лежат на одной прямой, то у этих треугольников общая высота, опущенная из точки O. Отсюда следует, что площади этих треугольников относятся так же, как их основания:

Аналогично можно выписать еще два соотношения:

; и

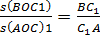
Перемножая эти три равенства получаем:

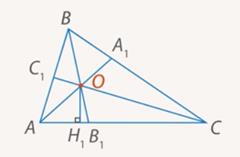
Рассмотрим левую часть данного равенства. Запишем её иначе.

Треугольники AOB1 и BOA1 имеют равные углы. Значит, их площади относятся как произведения длин сторон, заключающих эти углы.

То есть:

Аналогично можно выписать еще два соотношения:

и .

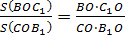
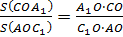
Перемножив эти равенства, получаем:

.

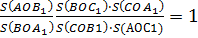
Имеем:

Докажем обратное утверждение.

Пусть точки C1, A1, B1 взяты на сторонах так, что выполнено равенство:

(1)

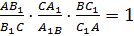
Докажем, что отрезки AA1, BB1, CC1 пересекаются в одной точке.

Обозначим буквой O точку пересечения отрезков AA1 и BB1 и проведем прямую CO. Она пересекает сторону AB в некоторой точке, которую обозначим C2. Т.к. отрезки AA1, BB1 и CC2 пересекаются в одной точке, то, по доказанному в первом пункте: 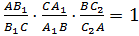(2)

Сопоставляя равенства (1) и (2): ,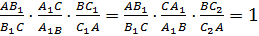

приходим к равенству 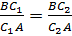; которое показывает, что точки C1 и C2 делят сторону AB в одном и том же отношении. Следовательно, точки

C1 и C2 совпадают, и, значит, отрезки AA1, BB1 и CC1 пересекаются в точке O.

1.2 Теорема Менелая

1.2.1 Кто такой Менелай? Древнегреческий математик и астроном. Автор работ по сферической тригонометрии: 6 книг о вычислении хорд и 3 книги «Сферики» (сохранились в арабском переводе). Для получения формул сферической тригонометрии использовал теорему о прямой, пересекающей стороны треугольника (теорема Менелая).

1.2.2 Формулировка и доказательство теоремы Менелая

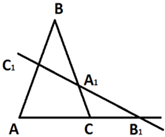
Дан треугольник ABC. На прямых AB, BC и AC отмечены точки C1, A1 и B1 соответственно. Точки C1, A1 и B1 лежат на одной прямой тогда и только тогда, когда:

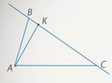
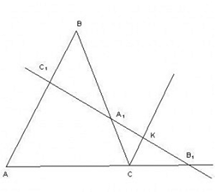
1. Проведем через точку C прямую, параллельную AB. Обозначим через K ее точку пересечения с прямой B1C1.

Треугольники AC1B1 и CKB1 подобны по двум углам.

Следовательно, .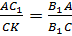

Далее, перемножив полученные равенства, получим:

,откуда следует, что:

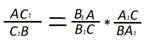
или :

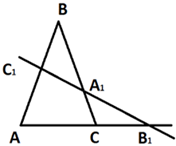
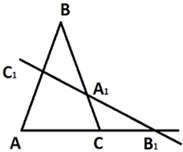
Докажем, что точки A1, B1, C1 лежат на одной прямой. (рис.2)

Прямая B1C1 пересекает сторону BC в некоторой точке A2. (рис.1)

Т.к. точки B1, C1, A2 лежат на одной прямой, то по доказанному в первом пункте:

Сопоставляя (1) и (2), приходим к равенству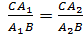, которое показывает, что точки A1 и A2 делят сторону BC в одном и том же отношении. Следовательно, точки A1 и A2 совпадают, и, значит, точки A1, B1, C1 лежат на одной прямой.

С помощью теорем Чевы и Менелая нетрудно доказать теоремы о четырех замечательных точках треугольника, теоремы Ван-Обеля и Симпсона. Остановимся на двух последних теоремах подробнее.

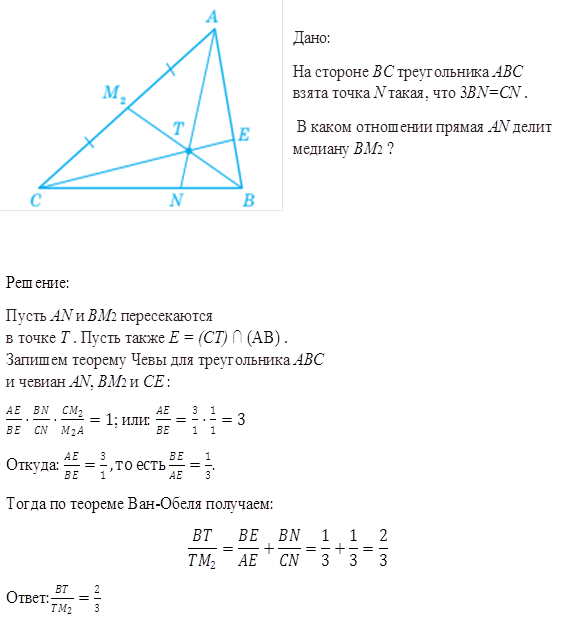
3.1 Теорема Ван-Обеля

Пусть чевианы AA1, BB1, CC1 треугольника ABC пересекаются в точке T, тогда справедливо равенство:

1.Для треугольника ABB1 и секущей CC1 запишем теорему Менелая:

; откуда получим (1)

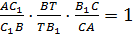
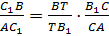
2. Для треугольника BB1Си секущей A1A, запишем теорему Менелая:

; откуда следует, что: (2)

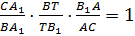
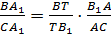
3. Сложив = .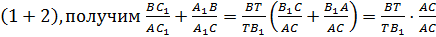

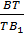
Итак, .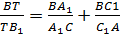

Теорема Симсона (Симпсона)

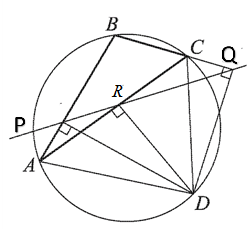
Пусть D – произвольная точка описанной около треугольника ABC окружности. DP, DR, DQ – перпендикуляры к сторонам AB, AC и продолжению стороны BC соответственно. Докажем, что основания перпендикуляров P, R, Q лежат на одной прямой

Основания перпендикуляров, проведенных к сторонам треугольника (или их продолжениям) из произвольный точки описанной окружности, лежат на одной прямой

Доказательство (Способ 1.)

Сделаем доп. построение – проведем отрезки AD и CD.

1) Т.к. ∠APD = 90° и ∠ ARD=90°,

то точки A,P,R,D лежат на одной окружности с диаметром AD.

Тогда ∠PRA = ∠PDA, т.к. они опираются на одну дугу.

то точки Q, C, R, D лежат на одной окружности с диаметром CD.

Следовательно вписанные углы ∠CRQ = ∠CDQ как опирающиеся на одну дугу.

Итак, ∠PDA = ∠QDC, следовательно, ∠PRA = ∠CRQ.

Это означает, что точки P, R, Q лежат на одной прямой.

Теорема доказана.

3.3 Решение задач с помощью теорем Чевы, Менелая, Ван-Обеля и Симпсона

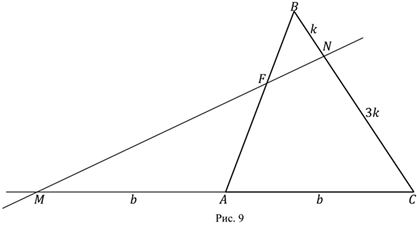
Дано: Три окружности с центрами А, В, С, радиусы которых относятся как 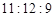, касаются друг друга внешним образом в точках X, Y, Z как показано на рисунке 19. Отрезки AX и BY пересекаются в точке O. В каком отношении, считая от точки B, отрезок CZ делит отрезок BY?

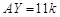
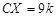
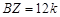
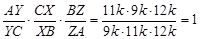
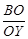
Решение. Обозначим , , (рис. 19). Так как , то по утверждению б) теоремы Чевы отрезки АX, BY и СZ пересекаются в одной точке — точке O. Тогда отрезок CZ делит отрезок BY в отношении . Найдем это отношение.

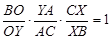
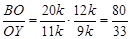
По теореме Менелая для треугольника BCY и секущей OX имеем: , откуда следует, что .

Ответ. .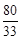

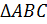
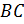
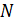
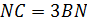
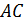
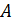
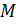
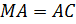
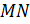
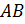
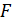
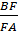
В на стороне взята точ­ка так, что . На продолжении стороны за точку взята точка так, что . Пря­мая пересекает сторо­ну в точке . Найти отношение .

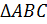
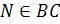
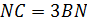
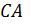
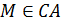
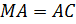
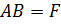
Дано: , , , – луч, , , .

Найти отношение .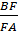

Решение. I способ (без использования теоремы Менелая).

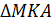
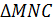
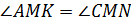
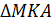
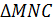
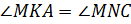
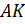
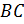
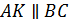
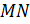
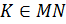
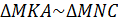
1) Рассмотрим и .

– общий угол для и ;

как соответственные углы, образованные при пересечении параллельных прямых и ( по дополнительному построению) секущей , . Следовательно, по двум углам.

Итак, 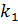– коэффициент подобия:

И, значит,

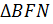
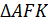
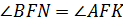
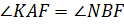
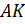
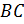
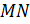
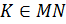
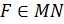
2) Рассмотрим и .

как вертикальные углы;

как накрест лежащие углы, образованные при пересечении параллельных прямых и секущей , , .

Следовательно, 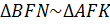по двум углам.

Итак, 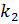– коэффициент подобия:

Но, так как по доказанному: 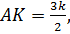то мы получаем, что:

Ответ: .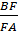

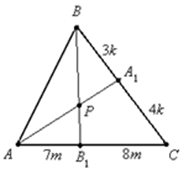
II способ (с использованием теоремы Менелая)

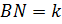
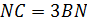
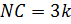
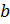
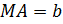
Пусть , тогда по условию (): ; пусть , тогда по условию МС= .

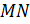
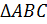
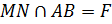
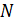
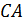
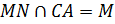
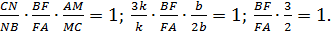
Прямая пересекает две стороны (, ) и продол­жение третьей ( – луч, ), значит, по теореме Менелая: И, значит,

Ответ: .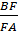

Как видим, использование теоремы Менелая значительно упрощает решение этой задачи.

Приложение. Банк задач, для решения которых рекомендуется использовать теоремы Чевы, Менелая, Ван-Обеля и Симпсона

Катеты прямоугольного треугольника равны 9, 12 и гипотенуза равна 15. Найдите расстояние между точкой пересечения биссектрис и точкой пересечения медиан.

В треугольнике ABC медиана AK пересекает медиану BD в точке L. Найдите площадь треугольника ABC, если площадь четырехугольника KCDL равна 5.

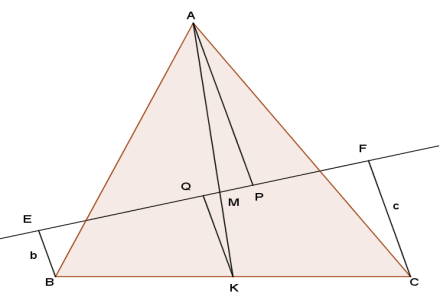
Через точку пересечения медиан треугольника ABC проходит прямая, пересекающая стороны AB и AC. Расстояния от вершин В и С до этой прямой равны b и с соответственно. Найдите расстояние от вершины А до этой прямой.

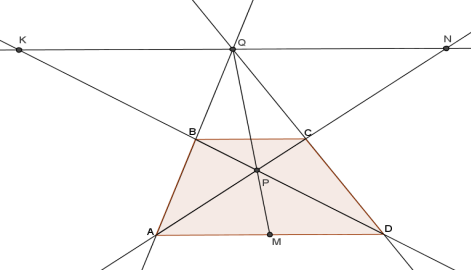
Прямая, соединяющая точку Р пересечения диагоналей четырехугольника ABCD с точкой Q пересечения прямых АВ и CD, делит сторону AD пополам. Докажите, что она делит пополам и сторону ВС.

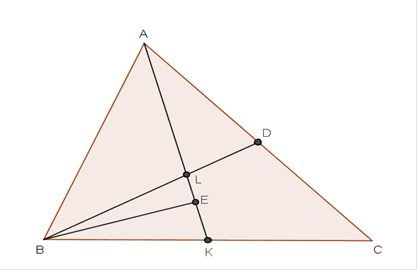
Из вершины С прямого угла треугольника АВС опущена высота СК, и в треугольнике АСК проведена биссектриса СЕ. Прямая, проходящая через точку В параллельно СЕ, пересекает СК в точке F. Докажите, что прямая EF делит отрезок АС пополам.

Источник