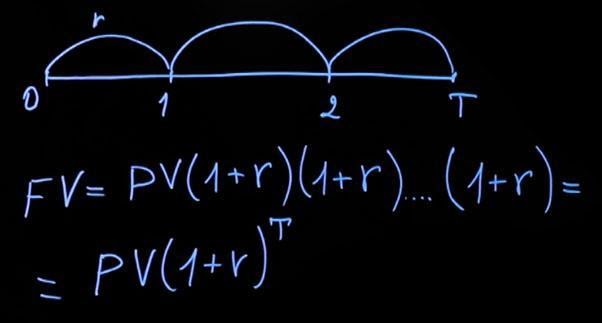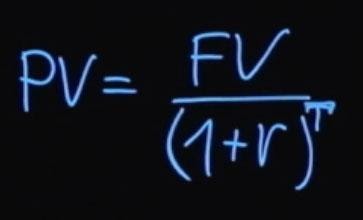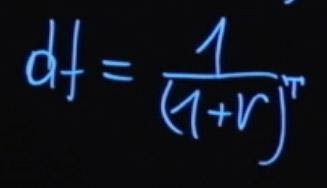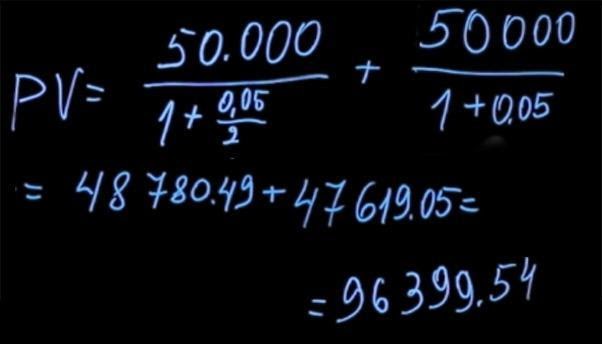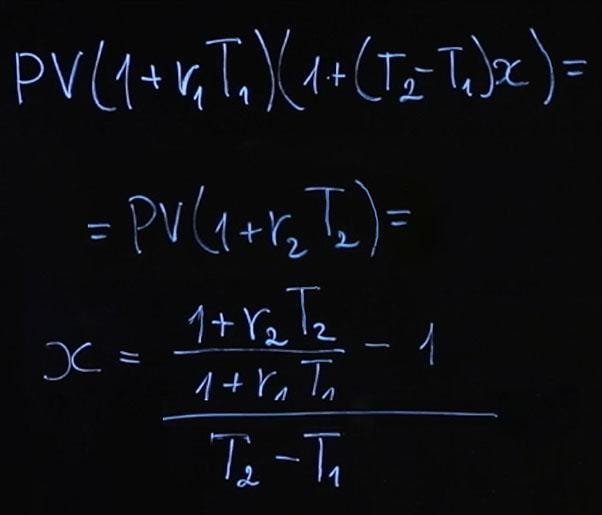чем выше ставка дисконтирования тем

Порядок определения ставки дисконтирования в соответствии с требованиями IAS 36 на практическом примере

Автор: Юлия Белогорцева, Партнер практики Оценки и инвестиционного консалтинга АКГ «ДЕЛОВОЙ ПРОФИЛЬ»

Опубликовано в журнале «Корпоративная финансовая отчетность. Международные стандарты»

Согласно IAS 36, ставка дисконтирования – это ставка, отражающая текущие рыночные оценки временной стоимости денег и рисков, характерных для данного актива, представляющая собой ту норму доходности, которую потребовали бы инвесторы, если бы они выбрали объект инвестирования, по которому денежные потоки, суммы, распределение во времени и структура риска были бы эквивалентны ожидаемым организацией к получению от актива. Стандарт содержит следующие требования, предъявляемые к ставке дисконтирования:

1. ставка должна отражать те риски, которые не были учтены в денежном потоке;

2. ставка дисконтирования не зависит от структуры капитала организации;

3. ставка должна быть доналоговой;

4. обычно используется постоянная ставка, однако, если ценность использования чувствительна к разнице рисков для разных периодов или к структуре сроков процентных ставок, применяется переменная ставка дисконтирования.

Стандарт отдает приоритет ставке дисконтирования, полученной непосредственно на рынке, однако, на практике, ввиду ограничения данной информации, для определения ставки дисконтирования используются суррогатные данные с учетом рекомендаций IAS 36 п. 55 А 17, согласно которым в качестве отправной точки может быть использована:

средневзвешенная стоимость капитала организации, определенная с использованием таких методов, как модель определения стоимости капитальных активов;

ставка привлечения дополнительных заемных средств организацией;

другие рыночные ставки по займам.

Таким образом, с учетом вышеизложенных рекомендаций стандарта для определения ставки дисконтирования используется модель средневзвешенной стоимости капитала – Weighted Average Cost Of Capital (WACC).

Средневзвешенная стоимость капитала (WACC) рассчитывается по формуле:

WACC – средневзвешенная стоимость капитала, %;

T – эффективная ставка налога на прибыль, доли ед.;

Dd – стоимость долга (cost of debt, стоимость привлечения заемных средств), %;

Wd – доля заемных средств, доли единицы;

De – стоимость собственного капитала, %;

We – доля собственных средств, доли ед.

Стоимость собственного капитала De (cost of equity) – доходность, которую инвесторы ожидают от инвестиций в собственный капитал.

Стоимость собственного капитала определяется по модели оценки капитальных активов (Capital Asset Pricing Model, CAPM):

Rf – безрисковая ставка, %;

β – коэффициент бета, доли единицы;

Rm – доходность на рыночный портфель, %

RiskA – риск, связанный с небольшим размером компании, %;

RiskB – страновой риск, %;

RiskC – специфический риск оцениваемой компании, %.

Далее рассмотрим порядок определения ставки дисконтирования на практическом примере для условной небольшой компании с капитализацией до 2,46 млн. долл. США, относящейся к отрасли Metals&Mining по состоянию на 01.08.2019.

Безрисковая ставка (Risk free rate) – норма отдачи, которую инвестор может получить на свой капитал при вложении в наиболее ликвидные активы, характеризующиеся отсутствием или минимальным возможным риском финансовых потерь.

В качестве безрисковой ставки целесообразно использовать доходность по государственным ценным бумагам с периодом обращения, близким сроку жизни основного актива генерирующей единицы. Для дальнейших расчетов была использована эффективная доходность по 20-летним казначейским облигациям США, которая по состоянию на 01.08.2019 г. составляет 2,21% (http://www.economagic.com/em-cgi/data.exe/fedbog/day-tcm20y).

Коэффициент Beta (β) – характеризует риск вложения в предприятия соответствующей отрасли и служит мерой систематического риска, с помощью которой может быть измерена амплитуда колебаний (неустойчивость) цен на акции какой-либо отдельно взятой компании по сравнению с изменениями на фондовом рынке в целом, для всех зарегистрированных компаний, которые образуют рынок.

Для расчета ставки дисконтирования необходимо принимать коэффициент β без учета долговой нагрузки (Unlevered Beta) с последующей корректировкой на финансовый рычаг. Формула для учета финансового рычага при расчете коэффициента β с учетом налогового «щита» приведена ниже:

βi – коэффициент бета, учитывающий финансовый рычаг;

βu – коэффициент бета, не учитывающий финансовый рычаг;

D/E – коэффициент, учитывающий соотношение «долг/собственный капитал» компании.

Коэффициент Beta (β) может быть определен самостоятельно как среднее значение по компаниям-аналогам или путем использования среднеотраслевых коэффициентов β, представленных в открытых источниках информации.

Коэффициент бета компании без учета долгового бремени определяется видом деятельности, которым занимается компания, и ее операционным рычагом. В качестве целевой структуры капитала необходимо использовать среднеотраслевые данные.

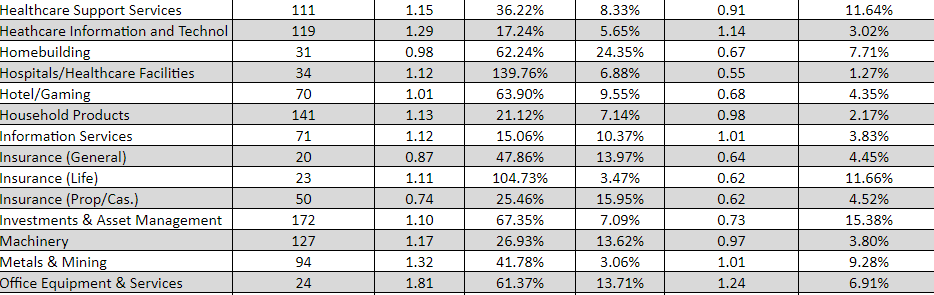
Для отрасли Metals&Mining на развитых рынках коэффициент бета составляет 1,01, а соотношение заемного и собственного капитала – 41,78% (http://pages.stern.nyu.edu/

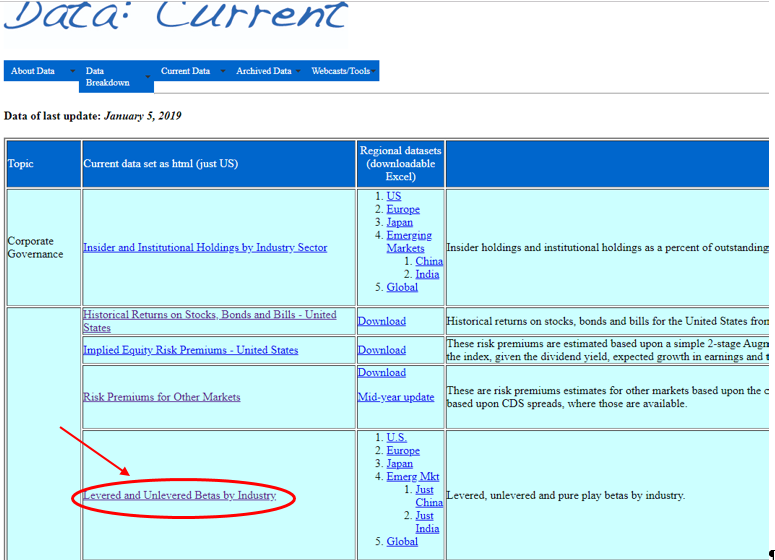
Ниже приведены копии интернет-страниц сайта damodaran.com с последовательностью шагов для определения Beta и соотношения «долг/собственный капитал»:

Шаг 1

Шаг 2

Шаг 3

Шаг 4

При расчете долгового коэффициента Beta (β) ставка налога на прибыль принимается на уровне 20,0%.

Таким образом, для дальнейших расчетов рычаговая Beta составит βi:

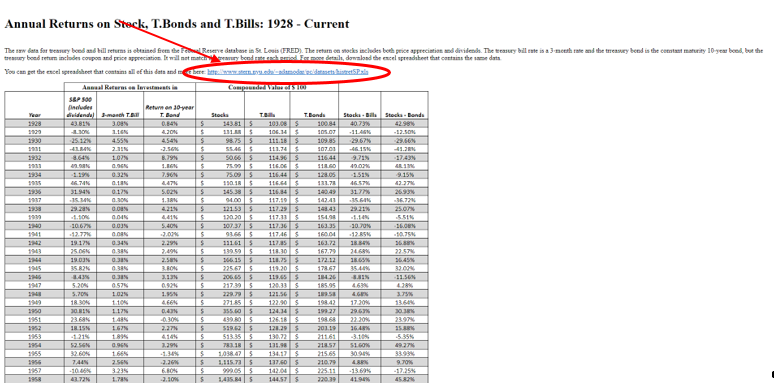
Рыночная премия за риск (цена риска) представляет собой разницу между ожидаемой доходностью рыночного портфеля и безрисковой процентной ставкой. Согласно сложившейся практике, в качестве рыночной премии за риск принимается разница между среднеарифметической доходностью акций и облигаций на американском фондовом рынке за период с 1969 по 2018 гг. (http://pages.stern.nyu.edu/

adamodar/). По указанным данным, рыночная премия за риск составляет 4%.

Ниже приведены копии интернет-страниц сайта damodaran.com с последовательностью шагов для определения размера рыночной премии за риск:

Шаг 1 и Шаг 2 идентичны последовательности, приведенной выше для определения Beta и соотношения «долг/собственный капитал».

Шаг 3

Шаг 4 (На указанной ниже странице есть возможность скачать рассчитанные данные в формате excel):

Премия за размер компании (size premium).

Результаты многочисленных исследований свидетельствуют о том, что у мелких компаний норма прибыли выше, чем у более крупных компаний. Так крупная компания имеет более легкий доступ к финансовым рынкам при необходимости привлечения дополнительных ресурсов, а также отличается большей стабильностью бизнеса, по сравнению с малыми компаниями.

Результаты исследований в этой области ежегодно обновляются и приводятся онлайн сервисом по подписке под названием The Cost of Capital Navigator (https://www.dpcostofcapital.com/).

Согласно приведенному выше источнику, премия за размер для компаний с микро-капитализацией в 2019 году составляет 5,22%.

Премии за страновой риск.

Премия за страновой риск отражает дополнительный доход, который ожидает инвестор за риск, связанный с вложениями в акции российских компаний, по сравнению с компаниями США. Страновой риск связан с неопределенностью получения доходов, которая вызвана возможностью изменения политической или экономической ситуации в стране.

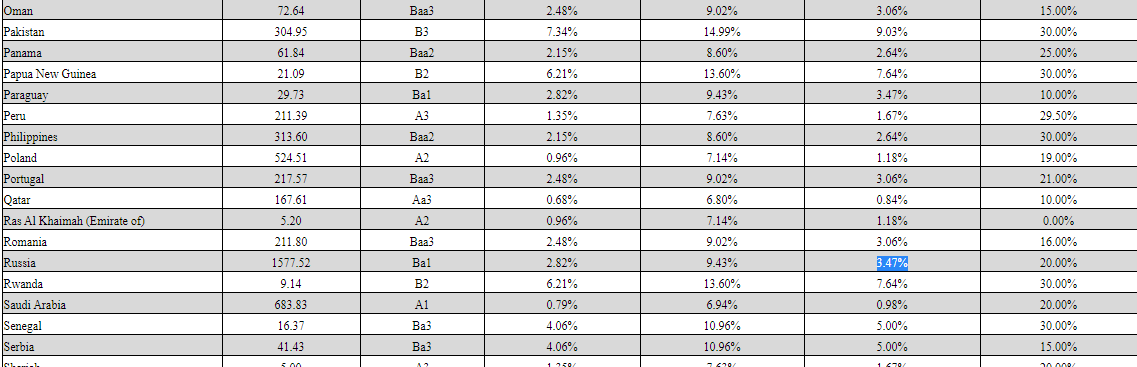
Для расчета премии за страновой риск можно использовать сведения, опубликованные на сайте А. Дамодарана (http://pages.stern.nyu.edu/

Согласно указанному источнику информации, размер премии за страновой риск для России (дата последнего обновления данных – январь 2019) составляет 3,47%.

Копия интернет-страницы сайта damodaran.com для определения размера премии за страновой риск представлена ниже:

Премия за специфический риск.

Премия за специфический риск отражает дополнительные риски, связанные с инвестированием в конкретное предприятие или конкретную генерирующую единицу. Премия за специфический риск оцениваемой компании может варьироваться в пределах от 0 до 5%.

Основными критериями, оказывающими влияние на специфический риск, являются: зависимость от ключевых сотрудников, зависимость от основных поставщиков и клиентов, эффективность корпоративного управления, состояние основных фондов, перспективы развития бизнеса и пр.

На практике премия за специфические риски не получила широкого применения, так как ее расчет может быть проведен только экспертно, на основе логики и опыта.

В случае стабильного функционирования компании и отсутствия существенных специфических рисков, по сравнению со среднеотраслевыми условиями, данная премия не учитывается. Для дальнейших расчетов размер премии за специфические риски был принят равным 0%.

После определения всех необходимых составляющих для расчета стоимости собственного капитала рассчитаем ставку CAPM:

De = 2,21% + 1,35 x 4% + 5,22% + 3,47% = 16,3%

Ставка CAPM, рассчитанная с учетом описанных выше компонентов, представляет собой требуемую ставку доходности для денежного потока, номинированного в долларах США.

Для возможности дисконтирования денежного потока, номинированного в рублях, необходимо полученную ставку скорректировать на валюту денежного потока, то есть долларовую ставку нужно перевести в рублевую.

Пересчет долларовой ставки в рублевую производится по следующей формуле:

Dруб – ставка дисконтирования для рублевого денежного потока;

Dдолл – ставка дисконтирования для долларового денежного потока;

rруб – доходность по рублевым государственным ценным бумагам;

rдолл – доходность по еврооблигациям России, номинированным в долл. США.

Доходность российских облигаций в долларах принята на уровне суммарного значения установленной безрисковой ставки и премии за страновой риск и составляет 5,68%.

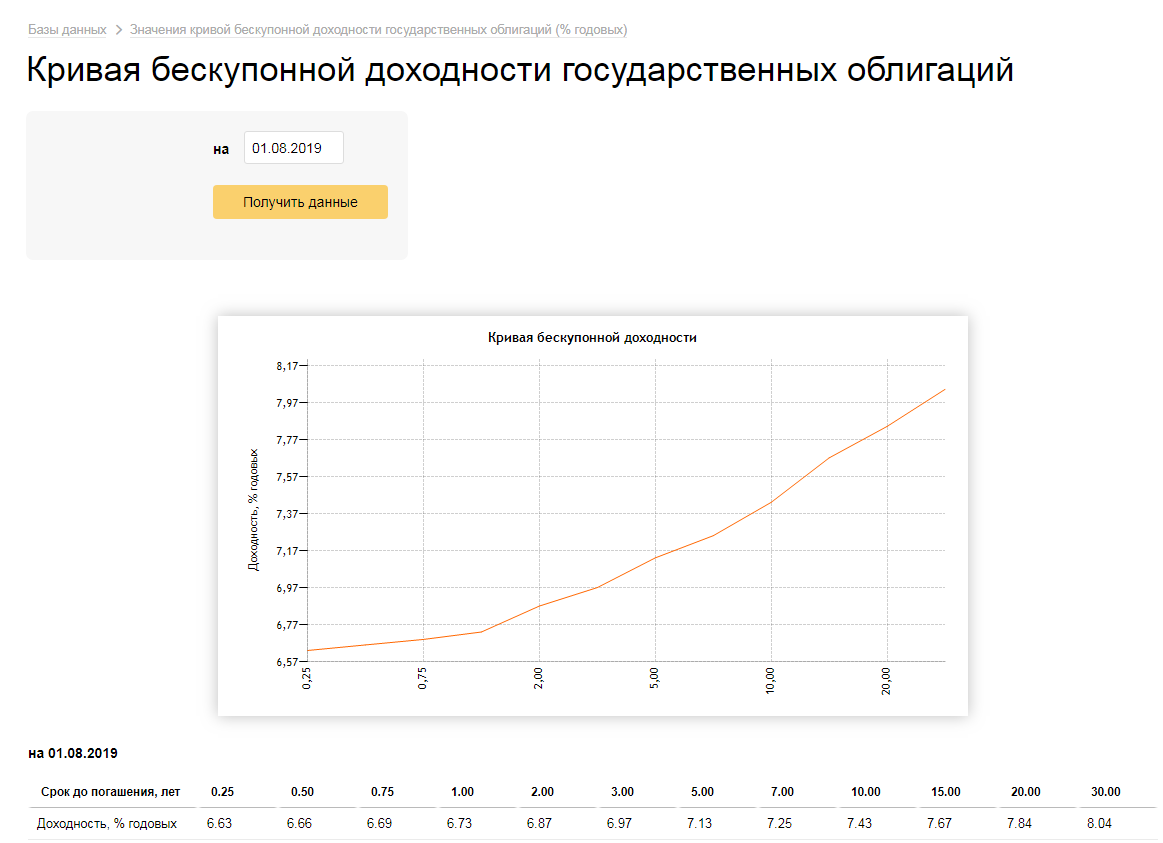
Доходность российских облигаций в рублях принята как значение кривой бескупонной доходности государственных облигаций по состоянию на 01.08.2019 со сроком погашения 30 лет (https://www.cbr.ru/hd_base/zcyc_params/zcyc/), которое составляет 8,04%.

Копия интернет-страницы сайта https://www.cbr.ru/ для определения бескупонной доходности государственных облигаций:

Тогда рублевая ставка составит:

Таким образом, стоимость собственного капитала составляет 18,9%. Для определения средневзвешенной стоимости капитала осталось определить стоимость заемного капитала, а также доли собственного и заемного капитала.

Стоимость заемного капитала (до налогов).

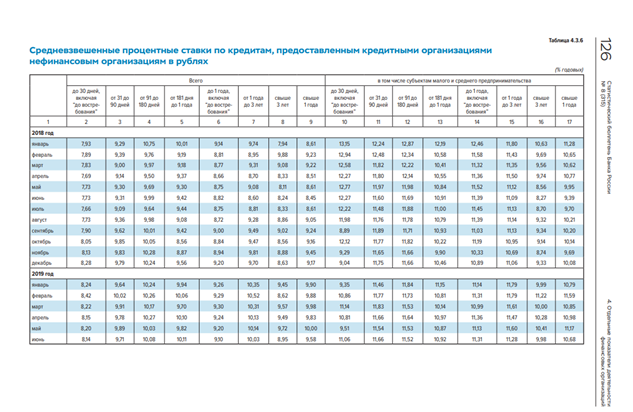
В качестве стоимости заемного капитала может быть принята средневзвешенная процентная ставка по кредитам, предоставленным кредитными организациями нефинансовым организациям в рублях на срок от 3 лет. Данная информация представлена в Статистическом бюллетене Банка России (https://www.cbr.ru/Collection/Collection/File/22637/Bbs_1908r.pdf). Согласно указанному источнику, величина средневзвешенной ставки по кредитам, предоставленным кредитными организациями нефинансовым организациям в рублях на срок от 3 лет составляет 8,95%.

Копия интернет-страницы сайта https://www.cbr.ru/ для определения средневзвешенной ставки по кредитам, предоставленным кредитными организациями нефинансовым организациям в рублях на срок от 3 лет:

Доля собственного капитала определяется по формуле:

We = 1 / (1 + D/E)

Тогда значение доли собственного капитала составит:

We = 1 / (1 + 41,78%) = 0,705

Значение доли заемного капитала составит:

Определенные выше составляющие позволяют определить средневзвешенную стоимость капитала (WACC):

Полученная ставка дисконтирования является номинальной рублевой посленалоговой.

Доналоговая ставка дисконтирования может быть определена по методу освобождения посленалоговой ставки дисконтирования от налога на прибыль:

Таким образом доналоговая ставка WACC составит:

Изложенный порядок определения ставки дисконтирования наглядно продемонстрировал, что этап ее определения один из самых сложных в процессе проведения теста на обесценение.

Для проведения тестирования на обесценение одним из наиболее часто используемых методов определения ставки дисконтирования является модель средневзвешенной стоимости капитала (WACC), при этом, в зависимости от даты, сферы деятельности компании, ее специфики, ставка дисконтирования может существенно отличаться.

Источник

Стоимость денег, типы процентов, дисконтирование и форвардные ставки. Ликбез для гика, ч.1

Представьте себе ситуацию – вы покупаете машину, и вам предлагают два варианта: заплатить с рассрочкой в несколько месяцев или погасить всю сумму сразу и с небольшой скидкой. Какой окажется выгоднее?

Или, например, вы хотите разместить вклад на год. Можно положить на весь срок под высокий процент или на отдельные короткие сроки под более низкий. Что лучше и насколько?

Все ответы под катом. И добро пожаловать в мир, где время — всегда деньги. До этого вы знали об этом, но теперь — в деталях и с примерами.

Меня зовут Мария Абрашкина, я математик и Product Owner в команде по расчету портфельных рисков. А также один из авторов видеокурса про финансовую математику (Ч.1 – Типы начисления процентов, Ч.2 – Дисконтирование, Ч.3 – Форвардные процентные ставки). В этом посте я расскажу о стоимости денег, процентных ставках и облигациях. Эти знания помогут вам в будущем принимать финансовые решения основываясь на точном расчете, используя простую математику.

#1. Временная стоимость денег. Типы начисления процентов

Сначала поговорим о том, что такое временная стоимость денег, или Time Value of Money (TVM), почему деньги имеют стоимость и какие виды процентов существуют.

На картинке ниже показан список фильмов с максимальными кассовыми сборами.

Можем ли мы их сравнить по этим цифрам? Учитывая, что фильмы выходили в разные годы, вряд ли такое сравнение будет правильным. Как быть?

Давайте рассмотрим более простой пример. Допустим, у вас есть тысяча рублей, и я у вас прошу эту сумму в долг. Сколько вы хотите, чтобы я вам отдала через год? Возможно, вы подумаете, что на эту тысячу рублей вы сейчас можете купить бутылку вкусного вина или что-то другое. Также вы можете предположить, что через год на ту же самую тысячу рублей вы вряд ли сможете купить этот товар по причине инфляции. Кроме того, существует риск, что деньги я не верну. Поэтому, скорее всего, вы захотите компенсацию за то, что вы пока не будете покупать бутылку вина или какую-нибудь другую вещь. Также вам необходим стимул, оправдывающий риск того, что деньги я вам могу и не вернуть. Вероятно, вы потребуете от меня вернуть деньги с какой-то надбавкой, то есть с процентом.

Итак, деньги имеют стоимость, потому что их владелец хочет компенсации за то, что он не может купить какой-то товар или услугу, и за риск, который он несет, давая деньги в долг.

На языке математики это будет выглядеть так:

Если записать эту формулу в общем виде, то будущее значение равняется сумме долга, умноженной на единицу плюс процентная ставка.

А что, если начисление процентов происходит не раз в год, а чаще? Или что если проценты начисляются в течение двух, трех, десяти лет? В данном случае нам нужно всегда уточнять, каким образом происходит начисление процентов, в конце срока или с какой-то периодичностью и на сколько лет.

Простые проценты

Рассмотрим пример, когда проценты начисляются в конце срока вклада. Будущее значение будет равняться текущему значению плюс текущее значение, умноженное на годовую процентную ставку. Годовая процентная ставка будет прибавляться к сумме нашего вклада столько раз, на сколько лет мы сделали вклад.

Если же процентная ставка начисляется каждый год, то формула будет выглядеть иначе.

Рассмотрим ситуацию с начислением за период в несколько лет. Считаем, что действующая процентная ставка на протяжении всего периода будет одинаковая. Тогда формула принимает следующий вид: текущее значение, умноженное на сумму единица плюс процентная ставка, затем еще раз на сумму единицы и процентной ставки и т. д. Умножать следует столько раз, на какое количество лет был сделан вклад. В общем виде формула будет выглядеть следующим образом:

Обратите внимание – если в первом случае к нашему вкладу каждый год прибавлялась сумма процентов (как в первом примере, где добавлялось к сумме вклада 50 рублей), то в случае с ежегодным начислением на 50 рублей, добавленные в первом периоде, у нас каждый раз начисляется процент.

Всегда важно обращать внимание на то, каким образом происходит начисление процентов. Проценты могут начисляться не только раз в год, но и раз в полгода, каждый день. И в принципе нам ничего не мешает начислять эти проценты непрерывно.

Непрерывное начисление процентов

Как же будет выглядеть формула, если мы хотим начислять проценты непрерывно? Тут придется вспомнить школьную математику. Формула будет следующей:

Для того, чтобы привести наш предел к какому-то удобному виду, нам нужно сделать подстановку. В итоге мы получаем следующее:

С учетом того, что наш предел равен числу Эйлера (е=2,71), наша формула преобразуется в очень простое выражение. Текущее значение нашего вклада умножается на экспоненту, которая возводится в степень, представленную произведением процентной ставки и количества лет, на которые начисляются наши проценты.

Давайте сравним, как выглядят платежи в зависимости от периодичности начислений. В таблице представлено будущее значение вклада в сто тысяч рублей, который положен на десять лет по ставке двадцать процентов.

Таким образом сумма вклада при начислении процентов ежегодно в два раза превышает сумму вклада при выплате процентов единожды в конце срока.

Если же начисления производятся непрерывно, то сумма вклада оказывается более 700 тысяч рублей против 300 тысяч рублей при простом начислении процентов.

На графике ниже наглядно показано, как растет итоговая сумма вкладов при разных способах начисления процентов.

Отсюда необходимо сделать вывод:

выбирая вклад, важно смотреть не только на размер процентной ставки, но и на периодичность начисления процентов. Высокая процентная ставка не всегда является по-настоящему выгодной.

Поэтому, перед тем как сделать свой выбор, имеет смысл сделать небольшие вычисления, чтобы узнать итоговую сумму вклада при заданных условиях.

#2. Дисконтирование (помогает понять, что лучше: взять рассрочку или заплатить сейчас со скидкой)

Мы рассмотрели, какие бывают ставки и какие бывают способы начисления процентов. Если проценты выплачиваются в конце срока действия вклада, проценты называются простыми, если проценты выплачиваются с какой-то периодичностью, то такие проценты называются сложными.

Давайте решим обратную задачу. Допустим, мы знаем, сколько нам заплатят в будущем (например, нам кто-то пообещал платеж за какой-то продукт). Мы также знаем, какая сейчас процентная ставка. Как нам посчитать текущую цену этого продукта?

Как было сказано ранее, будущее значение суммы платежа будет равняться текущему значению, умноженному на единицу плюс процентная ставка. Если из этой формулы мы выразим текущее значение, то оно будет равняться будущему значению, деленному на единицу плюс процентная ставка.

Если проценты начисляются с какой-то периодичностью, то в общем виде формула выглядит так:

Давайте вернемся к задаче о том, какую премию лучше выбрать. В зависимости от способа премирования сумма выплат может отличаться. При этом не всегда очевидно, какой из способов предпочтительнее. Чтобы дать правильный ответ, необходимо решить математическую задачу. Предположим, у нас есть возможность взять в конце года 105 тысяч рублей при процентной ставке 5 процентов. Либо мы можем выбрать другой способ премирования, когда нам выплачивают по 50 тысяч рублей раз в полгода при той же процентной ставке.

Сравним эти два платежа. Для этого посчитаем, какое будет текущее значение для каждой из данных выплат. Воспользовавшись формулой для нахождения текущего значения, нам нужно продисконтировать 105 тысяч по ставке пять процентов (в данном случае T=1). Получаем 100 тысяч.

Чтобы найти текущее значение выплат через каждые полгода, мы должны 50 тысяч рублей (которые получим через полгода) продисконтировать по ставке два с половиной процента (потому что начисление происходит только в первые полгода. Строго говоря, ставка на 6 мес не равна половине годовой ставки. N(1+x)(1+x)=N(1+0.05) => x=2.4695% мы инвестируем на 6 мес, а потом опять на 6 и это идентично инвестиции на год), пять процентов годовых, деленные на два, плюс 50 тысяч полученные в конце года, которые мы дисконтируем по ставке 5 процентов. В результате подсчетов мы получаем цену первого платежа за полгода в размере 48780 рублей 49 копеек и второго платежа — 47619 рублей 5 копеек. Сумма ценностей составляет 96399 рублей 54 копеек.

Выгоднее получить премию в 105 тыс рублей, подождав дольше.

Например, когда вам предлагают купить автомобиль в рассрочку или заплатить полную сумму сейчас с какой-нибудь скидкой. Нужно взять будущую сумму, которую вы заплатите, привести к текущему значению, а затем сравнивать платежи, происходящие в один и тот же момент времени.

В таком случае сравнение будет корректным.

#3. Форвардные процентные ставки

Допустим, мы с вами договоримся о процентной ставке. Под эту процентную ставку я через год возьму у вас деньги в долг, которые верну через два года плюс процент. Какова должна быть в данном случае процентная ставка, чтобы она была справедливой? Распишем этот пример подробнее.

Либо положить деньги сразу по ставке r ₂ на два года.

На финансовом рынке существует правило отсутствия арбитража (No-Arbitrage Condition). Оно говорит о том, что если в конце срока мы получаем одинаковые выплаты, то для инструментов с одинаковым риском начальная сумма должна быть тоже одинаковая. Давайте распишем и это. Будущее значение первого варианта инвестиции FV ₁ будет равняться текущему значению, умноженному на сумму единицы и rT ₁ (будем считать, что у нас простое начисление процентов).

Из этого мы получаем следующее:

Формула получилась достаточно громоздкая. Давайте рассчитаем по этой формуле пример, а затем подумаем, что мы можем сделать, чтобы она выглядела проще.

Пусть процентные ставки у нас r ₁=4%; r ₂=6%. В таком случае имеем следующее:

Казалось бы странно, что ставка на два года равняется шести процентам, на год она равняется четырем процентам, а от года до двух мы получаем ставку более семи процентов. Объясняется это так. Поскольку в первый год у нас годовая ставка ниже чем на два года, в следующий год она должна быть выше, чем обе этих ставки. Это необходимо для того, чтобы компенсировать недостаток начисления процентов в первом году, и после реинвестирования можно было бы получить такую же сумму, как при инвестировании на два года по более высокой ставке. Такая ставка называется форвардной процентной ставкой.

Чтобы облегчить себе жизнь, давайте упростим эту формулу. Если мы будем использовать формулу непрерывного начисления процентов ( FV=PVe rT ), то тогда мы можем переписать условие отсутствия арбитража следующим образом:

Если мы возьмем логарифм от обеих сторон нашего равенства и сократим константы, мы получим:

Далее легко найти x:

Согласитесь, такую формулу для будущих процентных ставок использовать гораздо проще и удобнее.

Вы можете задать вопрос – а зачем такой странный продукт и кто им пользуется?

Представьте себе ситуацию, когда у вас или у вашей компании точно будет поступление средств через год. Сейчас вы бы хотели обезопасить себя от риска изменения процентных ставок. Вы понимаете, что через год процентная ставка может увеличиться и стать более выгодной, но также вы понимаете, что она может понизиться. И вам вполне комфортно с действующей на рынке форвардной процентной ставкой. Тогда вы можете заключить контракт, указав в нем, что на те деньги которые поступят в будущем через год, вы заключаете договор по заданной ставке. Ставка фиксируется, и вы больше не переживаете о том, как будут происходить изменения процентных ставок на рынке.

Обратите внимание, что форвардная процентная ставка ни в коем случае не является предсказанием будущей цены. Это абсолютно не значит, что процентные ставки будут равны 7,7% через год, когда мы окажемся в точке T₁. Они могут принимать какое угодно значение, и вот почему. В момент, когда мы рассчитываем форвардную процентную ставку из ставок, действующих на рынке, мы можем сказать, что эта ставка является ожиданием рынка относительно будущих цен. Но к моменту, когда мы перемещаемся в будущее, происходят новые события, добавляется новая информация, и рынок каким-то образом меняется. Поэтому процентные ставки через год не будут совпадать с форвардными ставками, рассчитанными на год сейчас.

Источник