чем выше npv тем лучше
И IRR, и NPV работают на максимум. Чем больше, тем лучше



NPV – это сумма дисконтированного денежного потока.
В статике все кажется в шоколаде. В динамике же не так, по второму проекту получили минус.
В различной литературе для NPV существует несколько формул:
NPV = = = +
· Если NPV>0, то наши затраты окупились и дали прибыль – проект принимается.
· Если NPV 0 и проект принимается.
-2000 ++
Получится полином 5-ой степени без вариантов решения.
IRR не имеет формулы расчета его. Не имеет аналитического решения.
Решение находится численными итерационными методами.
От чего зависит значения IRR? ТОЛЬКО ОТ CF ПРОЕКТА. Пока какая-то циферка в потоке не изменится, то IRR не изменится. IRR – критерий абсолютный.
Два метода расчета IRR: 1. Упрощенная схема
| i |
| NPV |
| NPV1 |
| NPV2 |
Способы определения IRR:
1. Графический. Через электронные таблицы.
2. По упрощенным схемам 1 и 2. С разной степенью приближения.
3. Использование финансовых калькуляторов.
4. Финансовые функции любых электронных таблиц.
По проекту А: IRR > %-ой ставки. Не намного больше. IRR д.б. > 13% (12,898).
По проекту B: IRR в
Если PI>1, то проект принимается. Если PI PBP.
Когда говорим о сроке окупаемости, то нужно использовать не просто формулу, а алгоритм.
| t | |
| -20000 | -200000 |
| -16000 | |
| -10000 | |
| -4000 |
Построить нужно кумулятивный поток платежей (Cumulative – поток нарастающим итогом).
На конец 4-го года, я уже в плюсе. Проект окупился между 3-им и 4-м годом. Фиксируем номер периода PPS=3, после которого поменялся знак. Поступления равномерно. Беру отношение:
Здесь не нужна сумасшедшая точность.
| t | |
| -25000 | -25000 |
| -17000 | |
| -11000 | |
| -6000 |
года ровно (так как получили 0). В реальной жизни такого не бывает.
Здесь нет никаких средних. В одном потоке одно. В другом другое. Натянутых чисел нет.
Алгоритм расчета критерия:
1. ПО исходному потоку платежей строится поток нарастающим итогом .
2. Фиксируется номер периода, после которого поменялся знак в потоке.
3. К этому номеру периода добавляется отношение последней задолженности к поступлению следующего периода:
Динамический срок окупаемости Payback Period (ВPP) (PPD)
Абсолютно все то же самое, только должны построить дисконтированный кумулятивный поток.
| t | ||
| -20000 | -20000 | -20000 |
| 3571,43 | -16428,57 | |
| 4783,16 | -11645,41 | |
| 4270,68 | -7374,73 | |
| 4448,63 | -2926,10 | |
| 3404,56 | 478,46 |
Можно вывести формулу в общем виде. Она имеет страшный вид. С использованием аппарата алгебры множеств. «Формула Большой Иероглиф» 😀 А там таких 4 штуки =)
Если NPV разные анализы.
Математически доказано, что если потом ординарный, то график будет иметь классический вид графика1 и IRR будет иметь единственное значение. А если поток неординарный (если несколько раз меняется знак), то уравнение может иметь столько действительных корней, сколько раз меняется знак в потоке.
Тогда возникает следующий вопрос: что же такое произошло в 80-е годы, что стали появляться неординарные потоки? Множественность возникала, она не могла не быть. Но, существовали классические приемы ухода от множественности.
Есть какой-то поток:
Но, выделяли две очереди реализации проекта. Или брали же кредит.
Заканчиваются минусы, кредит под окончание проекта никто не даст. Этот способ стал не применим. В 80-е годы пошли инвестиционные проекты, в которых затраты шли в конце (затраты по завершению проекта).
Можно всегда подобрать математическую модель (из Мат. Анализа) с затухающими колебаниями
2. Критерий IRR завышает требования к ставке реинвестирования доходов от проекта, предполагая, что средство реинвестируется по ставке, равной IRR, что в практической жизни, как правило, невозможно.
Возьмем все оттоки, каждый продисконтируем (приведем все затраты к началу). Значит, можем найти сумму.
| TV |
Это мы рассчитать всегда можем. Дальше возьмем все значения, со знаком «+». И свой доход мы будем копить до конца срока реализации проекта:
Если это сегодняшняя, а это будущая. Как их прировнять? Найти ставочку, которая приведет будущую к сегодня.
Критерий MIRR – это ставка, которая уравнивает наши накопленные доходы и дисконтированные поступления.
В более коротком виде, если расписать:
Рассмотрим на это уравнение с точки зрения целей, которые ставились перед разработчиками. MIRR всегда существует и имеет единственное значение? И PV, и TV положительные, значит единственное значение. С точки зрения классической алгебры, не всегда существует. Когда под радикалом меньше 1, тогда не будет иметь смысла (т.е. TV
Посмотрим с точки зрения экономики. Что за проект, для которого TV
Если взять формулу (1). В классическом варианте она написана не так:
Пишется ставка финансирования, по которой я привлекаю источники финансирования ( )
А там ставка реинвестирования ( ), доступны какие-то источники (инструменты), куда я могу инвестировать доходы от проекта.
Критерий MIRR рассчитывается при равенстве ставок финансирования и реинвестирования:
Т.е. соблюдаются равные условия.
Но на основе критерия, можно рассчитать показатели. Показатель MIRR может быть рассчитан при неравенстве ставок.
Первую задачу решили. Ушли от множественности. И вторая задача учтена.
Если MIRR выше ставки дисконтирования (i), то проект принимается. Если ниже, то отвергается. Если равен 0, то проект может быть принят, так как не приносит убытков.
Соотношение значений между MIRR и IRR.
Если NPV по заданной ставке дисконтирования, то IRR будет всегда больше, чем MIRR. А если NPV отрицательно, то MIRR > IRR.
Задача: Предприятие собирается приобрести грузовик за 120к евро. Каждый год ожидается поступление от эксплуатации по 60к. Текущие эксплуатационные расходы составляют 30к в год. ПО истечении срока эксплуатации, равного 5 года, грузовик можно продать за 20к. Ставка по альтернативным вложениям капитала 10% годовых. Эффективна ли данная инвестиция?
Т.е. мы должны рассчитать все значения критериев эффективности.
| t | Отток | Приток |
| -120000 | -120000 | |
| -30000 | ||
| -30000 | ||
| -30000 | ||
| -30000 | ||
| -30000 |
Возмещение инвестиционных затрат
| t | Остаток на начало периода | Чистые поступления по проекту | Ожидаемые платежи по %-ой ставке | Возвращение вложенных сумм | Долг на конец |
| 3=1*i | 4=2-3 | 5=4-1 | |||
| -102000 | |||||
| -82200 | |||||
| -60420 | |||||
| -36462 | |||||
| 3646,2 | 46353,8 | 9891,8 |
На самом деле 30000 – не все мои. А 12000 можно было бы получить, не шевеля пальцами. А там, 12000 заработали деньги, а 18000 – я.
Получим 9891,8,а NPV у нас 6142,03. Какая цифра верная? NPV – это сегодня, а 9891,8 – это завтрашние. Деньги сегодня дороже денег завтра. Так что они обе верные =)
ВЫВОДЫ:
2. Сумму, равную NPV я никогда в руках держать не буду. Это чисто расчетная величина, так как же как и IRR.
3. Если NPV проекта положительно, то инвестор получает назад:
3.1. Свой вложенный капитал
3.2. Плюс %-ы по этому капиталу
3.3. И доход, равный NPV
Вернем свои деньги с %-ми и NPV, которые говорят на сколько я получу больше, чем если деньги будут лежать в банке.
Эта таблица имеет важное значение.
Анализ инвестиционных проектов с различными жизненными циклами.
Рассмотрим на примере. Есть 2 проекта C и F. И даны потоки платежей.
С точки зрения прироста стоимости фирмы предпочтение должно быть отдано проекту C, т.к. он генерирует большее значение NPV. Но 7165 будет реализовано через 6 лет, а 5391- через 3 года. Поэтому сравнение не совсем корректное. Нужно решить что лучше. Теоретики предлагают 3 метода решения:
1. Метод цепного повтора.
2. Методы эквивалентного аннуитета.
3. Метод вечной ренты.
Метод цепного повтора.
Сущность: предполагаем, что более короткий проект можно повторить второй раз. Строится гипотетический проект платежей F’. И выйдем на равные ЖЦИ. И по этому «двойному потоку» рассчитываем NPV. Сам поток неординарный, но у IRR множественности не возникает.
Делается вывод: так как NPV потока F’ больше, чем у C, то предпочтение должно быть отдано более короткому проекту F.
А с какой кстати будем повторять проект второй раз?
Сформулируем алгоритм в общем виде. Если есть 2 потока с разными ЖЦИ, то
1. Рассчитать наименьшее общее кратное ЖЦ проектов. (Получается 6)
3. Тот проект, сгенерированный поток которого даст большее значение NPV, признается более выгодным.
1. Проект не возможно и не нужно повторять несколько раз
2. Потоки изменяются, цифры не остаются такими же
Метод эквивалентного аннуитета.
Суть: исходный инвестиционный поток заменяется эквивалентными ему по NPV рентным потоком платежей. Проект, у которого значение аннуитета будет большим, считается лучшим.
1. Рассчитывается NPV исходных проектов
2. Рассчитывается коэффициент ренты или коэффициент аннуитета
3. Рассчитывается значение эквивалентного аннуитета EAA (Equivalent Annual Annuity).
4. Там, где ЕАА больше, тот проект лучше.
Метод вечной ренты (бесконечного цепного повтора).
Суть: предполагается, что доход, равный ЕАА, мы можем получать бесконечно долго. То есть проект будет повторяться бесконечно долго. И мы можем вычислить стоимость вечной ренты (Perpetuity).
Если рассчитаем по проектам:
Тот, который генерирует большее значение вечной ренты, считается лучшим.
По всем трем методам получили, что проект F лучше.
Если внимательнее посмотрим, то увидим, что все считалось по разным циклам. (3 и 6 лет). Где логика.
Суть метода, исходный поток заменяется эквивалентным по NPV рентным потоком. (5 и 6 столбики).
А если рассчитать NTV этих проектов?
| Год | C | F |
| -400000 | -20000 | |
| IRR | 17,5% | 25,2% |
А NTV по проекту F будем считать исходя из того, что после 3-х лет доходы будем класть в банк, поступления нулевые.
Получается проект С лучше. Сточки зрения формальной логики, NTV более применим к проектам с разными ЖЦ.
Мы тут не учли, что эти проекты разные по масштабам инвестирования. Эти проекты так напрямую сравнивать нельзя. Отличия в 2раза!
В программе “ProjectExpo” расчета эффективности инвестирования считается показатель D (длительность). D – это показатель, который характеризует величину чистого денежного потока, создаваемого проектом. Его можно интерпретировать как средний период времени до момента, когда проект начинает давать прибыль. (Расчет идет по дисконтированному потоку)
— чистый денежный поток месяца t и месячная ставка дисконтирования
PV – суммарный денежный поток проекта, который рассчитывается по формуле
Противоречия критериев эффективности
Возникают, когда мы рассматриваем 2 или более проектов. По одному критерию один проект лучше, по второму – другой и так далее. Рассмотрим 2 случая возникновения противоречий:
1. Точка Фишера – анализ альтернативных проектов.
Есть 2 проекта А и В.
| t | А | В | В-А |
| -100 | -100 | ||
| -80 | |||
| IRR | 29,96% | 20,44% | 9,52% |
Если построим графики зависимости NPV от %-ой ставки.
| 10% 20% 30% i |
| NPV |
| А |
| В |
Точка пересечения поделила нашу ось абсцисс на 2: при меньшей ставке – проект В лучше, при большей – проект А. Эта точка носит название точки Фишера – это такая %-ая ставка, при который NPV проектов равны. И соответственно, если ставка дисконтирования выше, то выгоден один объект, и наоборот. Нужно проверять есть ли она. Могут пересекаться ниже ОХ, или не пересекаться вообще. Возникает вопрос такой: как найти координаты точки Фишера? Мы должны построить приростный поток В-А, поскольку реально проекта нет. И найти IRR этого проекта.
2. Анализ проектов, разных по масштабу инвестирования.
Это противоречие вот из-за чего проистекает: критерий IRR по своей природе не учитывает масштаб инвестирования.
Рассмотрим два проекта, которые берутся на 4 года
| t | A | B | А-В |
| -700000 | -100000 | -600000 | |
| IRR | 16% | 21,9% | 15% |
С точки зрения теории стоимости фирмы, предпочтение должно быть отдано проекту А, т.к. оно генерирует бОльшее значение NPV.
Но проект А в общем-то генерирует более высокий доход из-за того, что масштаб проекта больше.
В этом случае, нужно приростный поток, где из более емкого вычитают менее емкий.
Про IRR ничего не можем сказать, а NPV – просто разница значений.
Ну, рассчитали. А дальше что?
Формирование (оптимизация) портфеля инвестора
| Оптимизация портфеля инвестора |
Мы имеем ввиду портфель реальных инвестиций.
| Пространственная оптимизация |
| Временная оптимизация |
| Проекты поддаются дроблению |
| Проекты не поддаются дроблению |
Постановка задачи. У нас есть несколько инвестиционных проектов, которые удовлетворяют нас по значениям основных критериев эффективности. То есть нам бы хорошо реализовать все эти проекты. Но денег на реализацию всех проектов не хватает. Какие проекты мы должны включить в портфель инвестора, что суммарный NPV портфеля был максимальным? И возникают случаи:
1. Пространственной оптимизации, если проекты поддаются дроблению. Это означает, что можно не только целиком реализовать какой-то проект, но и любую его часть. При этом к рассмотрению берется соответствующая доля инвестиций и поступлений. Алгоритм:
1.1. Проекты ранжируются по критерию индекса доходности PI по убыванию.
1.2. В инвестиционный портфель включаются первые k-проектов, которые могут быть полностью профинансированы.
1.3. Очередной k+1-ый проект включается в портфель не в полном объеме, а лишь в той части, в которой он может быть профинансирован, то есть по остаточному принципу.
Пример: предположим, что предприятие может инвестировать: а) до 55млн. руб., б) до 90млн. руб. Цена источника финансирования – 10% годовых. И есть 4 проекта, каждый на 4 года.
| t | А | Б | В | Г |
| -30 | -20 | -40 | -15 | |
| 2,51 | 2,68 | 4,82 | 1,37 | |
| IRR | 13,4% | 15,6% | 15,3% | 13,9% |
| PI | 1,084 | 1,134 | 1,121 | 1,091 |
| Проект | Инвестиции | Доля инвестиций, включающаяся в портфель | Доля NPV |
| Можем потратить 55млн. | |||
| Б | 100% | 2,68 | |
| В | 35 (5) | 87,5% | 4,22 |
| 6,90 | |||
| Можем потратить 90млн. | |||
| Б | 100% | 2,68 | |
| В | 100% | 4,82 | |
| Г | 100% | 1,37 | |
| А | 15 (15) | 50% | 1,255 |
| 10,125 |
2. Если проекты не поддаются дроблению, то рассматриваются все возможные сочетания, которые проходят по финансированию. Задача решается прямым счетом. Выбирается комбинация с наибольшим значением NPV.
| Вариант | Суммарные инвестиции | Суммарное NPV |
| Можем потратить 55млн. | ||
| А+Б | 30+20=50 | 2,51+2,68=5,19 |
| А+Г | 30+15=45 | 2,51+1,37=3,88 |
| Б+Г | 20+15=35 | 2,68+1,37=4,05 |
| В+Г | 40+15=55 | 4,82+1,37=6,19 |
Этот метод ругают теоретики. А если проектов 100? Слишком много переборов. Что это за фирма, у которой денег не меряно и есть 100 проектов, которые ей нравятся? По любому по другим критериям будет отобрано 20, из которых уже нужно выбирать.
3. Временной оптимизации.Есть несколько проектов, которые нас устраивают, денег на все сразу не хватает. НО есть уверенность, что во второй год недостающие деньги будут в нашем распоряжении. В первый год есть 70млн., а во второй год у нас будет еще 35млн. Как распределить начала реализации проектов по двух годам, чтобы суммарное NPV портфеля было максимальным? (Эта ситуация гораздо более жизненная)
В основе методики составления портфеля в данном случае заложена идея: по каждому проекту рассчитывается специальный индекс, который учитывает относительную потерю NPV в случае, если проект отложен к исполнению на год. Проекты с минимальными значениями индексов могут быть отложены на следующий год.
Рассмотрим следующую табличку:
| Проект | NPV | Коэффициент дисконтирования (10%) | NPV, отложенное на год | (потери в значении NPV) | Величина отложенной инвестиции | Индекс возможных потерь |
| 5=2-4 | 7=5/6 | |||||
| А | 2,51 | 0,9091 | 2,28 | 0,24 | 0,0077 | |
| Б | 2,68 | 0,9091 | 2,44 | 0,24 | 0,0120 | |
| В | 4,82 | 0,9091 | 4,38 | 0,44 | 0,0110 | |
| Г | 1,37 | 0,9091 | 1,25 | 0,12 | 0,0080 | |
| 11,38 |
| Проект | Инвестиции | Доля инвестиций, включаемая в портфель | NPV портфеля |
| 1 год | |||
| Б | 100% | 2,68 | |
| В | 100% | 4,82 | |
| Г | 10 (5) | 66,(6)% 67% | 0,92 (=1,37*0,67) |
| 8,42 | |||
| 2 год | |||
| Г | 33% | (1,25*0,33=)0,47 | |
| А | 100% | 2,28 | |
| 2,69 |
NPV портфеля составит 8,42+2,69=11,11млн.руб. А если бы реализовали сразу все, то было бы 11,38млн.руб. Наши потери составили 0,27млн.руб.
Механизм сам по себе хороший, но на практике не все проекты поддаются дроблению. Но из всех перечисленных алгоритмов этот реальнее всех.
Формирование потоков платежей инвестиционного проекта.
На первом этапе рассматривается без учета финансирования. И эта сумма называется Free Cash Flour (свободный (чистый) поток платежей). Почему не берем? На первом этапе мы должны оценить будем ли мы заниматься этим проектом, а для этого нужно знать наши инвестиции, не важно, откуда берутся, окупятся ли она? Способен ли сам проект? Не задаемся вопросом, откуда деньги. Нужно доказать себе и потенциальному инвестору, что проект жизнеспособен и им стоит заниматься. Что проект имеет право на существование.
А на втором этапе уже нужно доказать банку (инвестору), что проект реально приносить доход, который принесет достаточную прибыль.
В технологии расчета заложен нормальный здравый смысл.
Структура операционного потока платежей
(Operational Cash Flour/Cash Flour From Operation (CFFO)).
Под операционной деятельностью понимается основная производственная деятельность. Операционный поток – это поток от основной производственной деятельности предприятия.
Основная производственная деятельность включает поступления и использования денежных средств, обеспечивающих выполнение основных производственно коммерческих функций.
Есть приток средства и отток средств.
| Притоки | Оттоки |
| Денежная выручка от реализации продукции, товаров, работ, услуг. | Платежи по счетам поставщиков и подрядчиков на материалы, услуги и т.д. – за все, что нам нужно для нашего производства. |
| Погашение дебиторской задолженности. | Выплата заработной платы на предприятии. |
| Полученные авансы. | Уплата налогов и т.д. |
| Поступление от продажи бартера (натуральный расчет). | Авансы уплаченные. |
| Согласно приказу МинФина к притокам относятся поступления по следующим доходным операциям: · Полученная арендная плата; · Комиссионное вознаграждение; · Прибыль от совместной деятельности; · Страховые суммы; · Штрафы, пенни, неустойки полученные; · Различные оприходованные денежные излишки. | Уплата процентов по кредиту снижающих налогооблагаемую базу. Что является источником погашения задолженности? Как отразится в бухгалтерии? Затраты на обслуживание долга из себестоимости, а часть относится на финансовый результат. По рублевым кредитам ставка рефинансирования(8,25%*1,8) можно погашать и включать в операционный поток. Но если мы брали кредит, скажем под 20%, то оставшуюся часть мы платим уже из чистой прибыли. |
| Сальдо операционного потока. Сальдо должно быть положительно – это основные доходы по проекту. Если оно отрицательное – то нужно думать, за счет чего же и где взять финансы. |
МСФО, Дипифр
Сравнение NPV и IRR. Модифицированная внутренняя норма доходности MIRR.

Так можно ли говорить о преимуществах одного метода над другим, и какой метод лучше?
Почему IRR так любят менеджеры?
На самом деле, нет ничего удивительного в том, что внутренняя норма доходности (IRR) чаще используется на практике. Этому есть простое объяснение:
Конечно же, первый пункт из этого списка самый важный. Потому что определение стоимости капитала для компании (так называемая WACC), которая используется при расчете NPV, само по себе является непростой задачей.
И да, высокое значение внутренней нормы доходности (например, 20%) производит сильное впечатление на слушателя и кажется заманчивым, однако все эти эпитеты из области эмоций. А инвестиции — это не та категория, которая может оцениваться на основе критериев «привлекательности».
В любом учебнике написано, что NPV метод предпочтительнее, так как он показывает величину добавочной стоимости, которую создает инвестиционный проект. IRR является относительным показателем, который показывает только при какой стоимости капитала мы получим нулевую добавочную стоимость. Может быть не стоит беспокоиться, и оба метода всегда дадут одинаковый ответ?
Когда методы NPV и IRR приведут к разным выводам?
Для независимых друг от друга проектов методы IRR и NPV всегда подскажут одно и то же решение: «принять» или «отклонить». Но мы живем в мире, где финансовые ресурсы (и не только они) ограничены. И всегда приходится выбирать между двумя взаимоисключающими проектами (построить дорогу в Якутии или отремонтировать мост в Волгограде). В этом случае нередки ситуации, когда метод IRR будет говорить нам, что стоит принять проект А, тогда как метод NPV будет «голосовать» за проект Б.
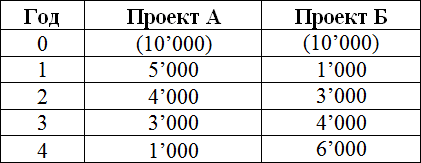
Возвращаясь к примерам из предыдущих статей про NPV и IRR, если проекты А и Б являются взаимоисключающими, то метод IRR всегда выберет проект А, так как 14,5%>11,8%. Но при ставке дисконтирования равной, например, 6% показатель NPV укажет на проект Б как на более предпочтительный:
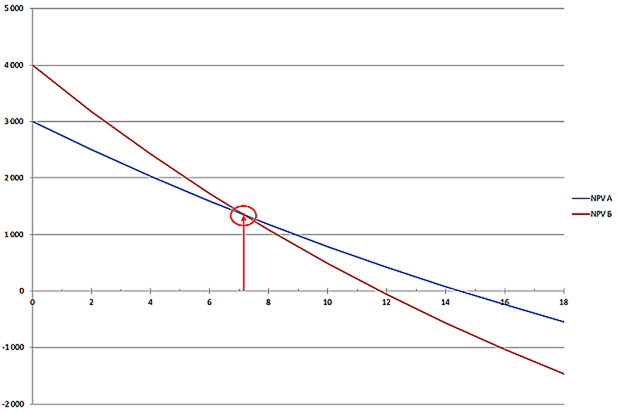
NPV и IRR будут рекомендовать разные проекты из двух возможных при стоимости капитала меньше, чем 7,2% (см. рис ниже).
Именно в этой точке (7,2%) графики зависимости NPV от ставки дисконтирования для проектов А и Б пересекаются между собой. Левее этой точки линия проекта Б ( красная ) выше, чем линия проекта А ( синяя ). Это значит, что при такой стоимости капитала (ниже 7,2%) проект Б сделает инвестора богаче, чем проект А.
О причинах такого положения дел я рассказывала в статье про расчет NPV инвестиционных проектов. Проект Б является долгосрочным, т.е. с течением времени денежные потоки от него увеличиваются. Проект А является краткосрочным с наибольшей отдачей в первые годы, а к концу проекта А поступления падают. Но чем дальше в будущее по времени от сегодняшнего момента, тем сильнее влияние ставки дисконтирования: через год увеличение ставки дисконтирования на 1% «съедает» 0,93% от денежного потока, а через 4 года рост ставки дисконтирование на 1% вызывает уменьшение денежного потока на 3,65%. Поэтому NPV долгосрочного проекта Б с ростом ставки дисконтирования падает быстрее, чем NPV проекта А, чьи денежные потоки максимальны в первые годы проекта. Это наглядно видно на рисунке: график проекта Б круче, чем график проекта А.
Получается, что методы NPV и IRR будут рекомендовать разные инвестиционные проекты, если есть разница по величине денежных потоков и по тому, как они распределены во времени: большие по величине в начале проекта или в конце. Это заложено в математику самого процесса дисконтирования.
Дело в том, что ставка дисконтирования работает в обе стороны времени — из будущего в настоящее (дисконтирование) и из настоящего в будущее (наращение). То есть если мы дисконтируем по 10% годовых, двигаясь из будущего к сегодняшнему дню, то мы можем и наращивать приведенные денежные потоки от сегодняшнего момента в будущее по этой же ставке. Внутренняя норма доходности, которую мы посчитаем методом IRR — это и ставка дисконтирования, и ставка инвестирования.
Так вот — когда мы рассчитываем IRR, мы предполагаем, что все денежные потоки инвестируются по этой ставке (как описано в примере про банковский депозит, его IRR равна ставке по депозиту).
Когда мы рассчитываем NPV, мы предполагаем, что денежные потоки дисконтируются и инвестируются по стоимости капитала компании. И это является более правильным с экономической точки зрения. Если мы получим IRR, равную 20%, это не означает, что мы можем найти банк или проект, который принесет нам ровно такую ставку доходности.
Все взаимоисключающие инвестиционные проекты с различающимися по времени денежными поступлениями правильнее сравнивать с помощью показателя NPV, который покажет вам прирост вашего богатства в абсолютной величине, а не потенциальную внутреннюю доходность, которую вы никогда, возможно, и не получите. Метод IRR для таких проектов может привести к неверному выбору, как в нашем примере при ставке 6%.
Еще достоинствах и недостатках метода IRR
Преимуществом показателя IRR является возможность оценить «запас прочности» проекта (safety margin) перед возможным увеличением процентных ставок. Например, в России кредитные ресурсы одномоментно стали дороже на несколько процентов, когда в ночь на 16 декабря 2014 года Центробанк РФ резко повысил ставку рефинансирования до 17%. Если бы мы приняли проект А, IRR которого равна 14,5%, то в этом случае он за одну ночь стал бы нерентабельным. А если бы мы нашли проект с внутренней нормой доходности равной 20%, то даже такое резкое увеличение процентных ставок не сделало бы наш проект убыточным.
К недостаткам метода внутренней нормы доходности относится тот факт, что для нестандартных проектов могут быть получены несколько величин IRR. Стандартный проект — это когда есть один отрицательный денежный поток в самом начале (первоначальная инвестиция) и несколько положительных денежных потоков в будущем. Если положительные и отрицательные денежные потоки будут чередоваться, то математически мы получим столько IRR, сколько раз денежные потоки от проекта поменяют знак.
Например, для проекта с такими потоками: (10,000), 5 000, (2 000), 4000, 5 000 будет получено два показателя IRR.
MIRR модифицированная внутренняя норма доходности — что это?
Анализ инвестиционных проектов на основе метода внутренней ставки доходности (IRR) предполагает, что все денежные потоки проекта могут быть инвестированы по этой ставке, что нереально. Этот недостаток метода IRR устраняется при использовании так называемой модифицированной внутренней нормы доходности или сокращенно MIRR (Modified Internal Rate of Return).
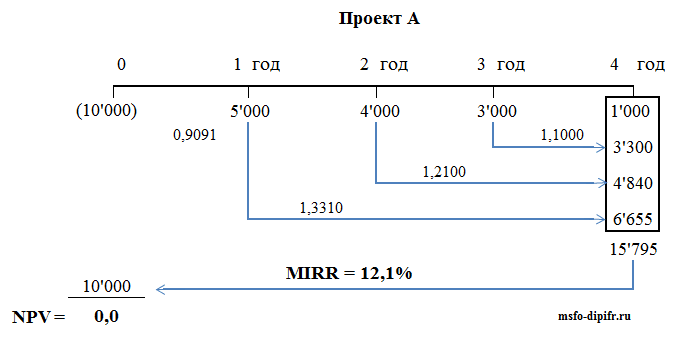
Суть расчета MIRR проста: все положительные денежные потоки от проекта наращиваются по % ставке, равной стоимости капитала компании (WACC), а затем находится ставка, дисконтируя по которой мы получим сумму нашей инвестиции. Возьмем для примера проект А, тот же самый, который использовался для расчета NPV и IRR ранее. Чтобы разобраться, как сделать расчет модифицированной внутренней нормы доходности, посмотрите на рисунок ниже:
Разберем всё по порядку.
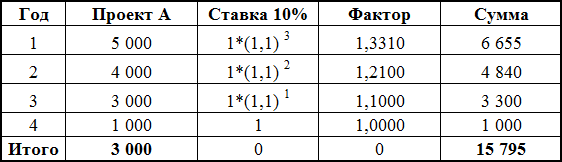
Действие первое: все потоки от проекта инвестируются (наращиваются) по ставке 10% (мы помним, что это стоимость капитала для нашей компании).
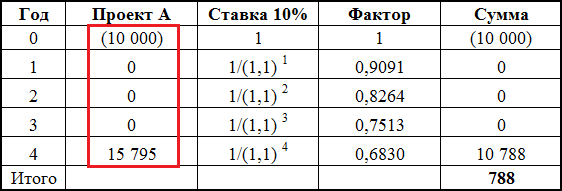
Последний денежный поток не наращивается, это будет датой окончания нашего инвестиционного проекта. Итого получилось в четвертый год суммарный денежный поток должен быть равен 15,795.
После этого денежные потоки от проекта будут такими (в красной рамке):
В этой таблице рассчитан NPV проекта после «модифицирования» его денежных потоков. Как видно из таблицы, ничего не поменялось: NPV проекта А как и раньше равно 788 денежным единицам.
То есть у нас получилось, что вместо ежегодных денежных притоков остался только один положительный денежный поток в конце 4-го года и первоначальная инвестиция в сумме 10,000. Единственный денежный приток является эквивалентом четырех ежегодных положительных денежных потоков, что подтверждается неизменностью величины NPV.
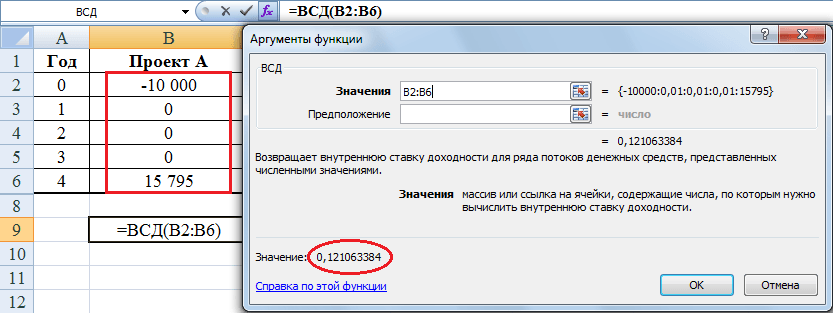
Действие второе: теперь надо вычислить внутреннюю норму доходности для этих двух денежных потоков, которые эквивалентны первоначальному проекту А. Для этого лучше всего воспользоваться функцией ВСД в программе Excel (об этом подробно рассказано тут):
IRR в данном случае получилось равной 12,1%, а не 14,5% как IRR для первоначального проекта А. Эта величина 12,1% и является модифицированной внутренней нормой доходности.
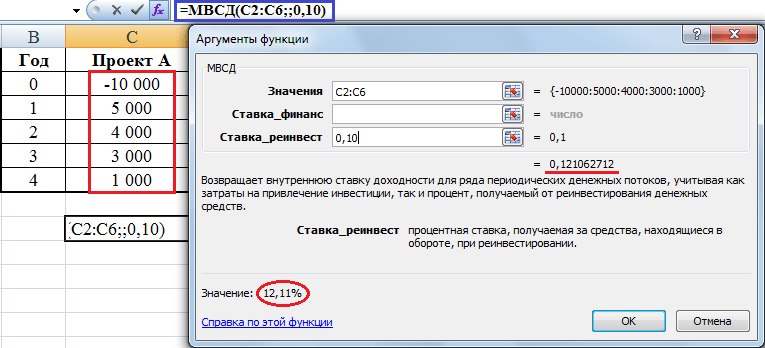
В программе Excel можно рассчитать показатель MIRR напрямую. В закладке Формулы—>Финансовые есть формула МВСД, которая и отвечает за расчет модифицированной нормы доходности. В ячейку «значение» нужно ввести ссылку на ячейки с денежными потоками, в ячейку «ставка_реинвест» — значение стоимости капитала, в нашем случае 10%.
Как видно из рисунка, функция МВСД дает то же самое значение показателя MIRR, которое было получено ранее расчетом из двух действий, а именно 12,1%.
Теперь можно посмотреть, как изменится решение о выборе из двух инвестиционных проектов А и Б.
Как видно из таблицы, при стоимости капитала (ставке дисконтирования и инвестирования) 10% оба метода «выбирают» проект А, при стоимости капитала 6% — оба метода также «голосуют» за один и тот же проект — проект Б (выделено синим). Сравните эту таблицу с предыдущей, где при тех же % ставках сведены вместе показатели NPV и IRR (ссылка на эту таблицу).
Таким образом, метод модифицированной внутренней нормы доходности снимает конфликт между NPV и IRR при выборе между двумя взаимоисключающими проектами, поскольку уравнивает ставку реинвестирования денежных потоков. Однако, MIRR отменяет одно из преимуществ метода IRR — придется рассчитывать ставку дисконтирования равную стоимости капитала компании, что всегда вызывает затруднения.
Возможность принятия противоположных решения также сохраняется. Если два проекта имеют одинаковый масштаб и продолжительность, то да, методы NPV и MIRR всегда будут выбирать один и тот же проект из двух взаимоисключающих проектов. То же самое справедливо и в отношении проектов одинакового размера, но разной продолжительности. В этом случае надо рассчитывать эти показатели на основе самого длительного проекта, просто добавив нулевые денежные потоки к более короткому проекту. Однако, если взаимоисключающие проекты различаются по масштабу (величине денежных потоков), то конфликт между двумя методами все еще возможен. Поэтому применение метода NPV все-таки является предпочтительнее, чем расчет IRR или MIRR (обычной или модифицированной внутренней нормы доходности).
«Сделай шаг, и дорога появится сама собой». Стив Джобс
Если вы раздумываете над тем, надо ли что-то сделать или следует получше подготовиться — не тратьте всю жизнь на сомнения. Можно бесконечно анализировать информацию, просчитывать варианты, оценивать риски и строить графики зависимости результата от самых разных показателей. Но всё дело в том, что точно предсказать будущее не может никто.
Вы можете всё время откладывать начало проекта в ожидании лучших условий — более низких ставок по кредиту, роста экономики, укрепления курса национальной валюты. Однако, не надейтесь, что дождетесь идеальных условий для старта, они никогда не наступят. Потому что когда исчезает одно препятствие, вместо него всегда появляется другое. Идеальный день для начала любого проекта — это сегодня.
«Теоретики беспокоятся о том, чтобы принять хорошее решение. В бизнесе мы так же беспокоимся о том, чтобы сделать решения хорошими».
Нужно принимать решение, опираясь на ту информацию, которая имеется в наличии сегодня. По дороге к мечте всё равно придётся вносить коррективы, чтобы добиться результата. Самый лучший прогноз всегда оказывается неверным. Потому что невозможно предсказать последствия как ваших действий, так и изменения окружающей обстановки с течением времени. Это можно сделать только в единственном случае — если вы ничего не делаете.
В мире бизнеса имеет значение результат, а не бизнес-планы. Впрочем, это относится к любым сторонам нашей жизни. Никого не интересуют мечты, важно, сумели ли вы до них дотянуться.
«Каждый раз нужно прыгать со скалы и отращивать крылья по пути вниз». Рэй Брэдбери
Лучше и не скажешь.
Другие статьи из рубрики «Финансы»: