чем выше модуль упругости тем
Модуль Юнга (упругости)
Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Основные сведения
Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м 2 или в Па.
Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (10 12 Па)
Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.
Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.
График теста на растяжение
E- это частное от деления нормальных напряжений σ на относительное удлинение ε.
Закон Гука также можно сформулировать и с использованием модуля Юнга.
Физический смысл модуля Юнга
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.
Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Величину, обратную α, и называют модулем Юнга:
Отношение растягивающей силы F к S называют упругим напряжением σ:
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l
Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Значения модуля юнга для некоторых материалов
В таблице показаны значения E ряда распространенных веществ.
| Материал | модуль Юнга E, ГПа |
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Графен | 1000 |
| Латунь | 95 |
| Лёд | 3 |
| Медь | 110 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 200/210 |
| Стекло | 70 |
Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.
Инструмент для определения предела прочности
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.
Связь с другими модулями упругости
Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:
E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.
Модуль деформации стали и её упругости

Общие понятия

Модуль Юнга в теории упругости обозначается буквой Е. Он является составляющей закона Гука (о деформации упругих тел). Эта величина связывает возникающее в образце напряжение и его деформацию.
Опытным путём осуществляется определение этого показателя в научных лабораториях. Сутью этого метода является разрыв гантелеобразных образцов материала на специальном оборудовании. Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости.
Таким образом определяется только модуль Юнга материалов упругих: медь, сталь и прочее. А материалы хрупкие сжимают до того момента, пока не появятся трещины: бетон, чугун и им подобные.
Механические свойства
Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала. А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:
Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства. Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.
У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.
Модуль упругости
Стоит отметить, что эта величина непостоянная. Даже для одного материала она может иметь разное значение в зависимости от того, в какие точки была приложена сила. Кое-какие пластично-упругие материалы имеют практически постоянное значение модуля упругости при работе как на растяжение, так и на сжатие: сталь, алюминий, медь. А есть и такие ситуации, когда эта величина измеряется формой профиля.
Некоторые значения (величина представлена в миллионах кгс/см2):
Разница в показателях модулей упругости для сталей в зависимости от их марок:
Ещё это значение изменяется в зависимости от вида проката:
Как видно, отклонения в значениях модулей упругой деформации стали незначительны. Именно по этой причине большинство инженеров, проводя свои расчёты, пренебрегают погрешностями и берут значение, равное 2,00.
7 шагов, чтобы посчитать модуль упругости стали
Модуль упругости стали: терминология + формула расчета + предел прочности и допускаемое механическое напряжение + 6 вспомогательных физических величин для инженерных расчетов упругости металлов + инструкция расчета модуля упругости стали на онлайн-калькуляторе.
Вспомните школьное время, когда вопрос «Где это нам пригодится в жизни?» звучал чуть ли не на каждом занятии. Для людей, связавших собственную жизнь напрямую/косвенно с металлургией, физика стала неотъемлемой частью практики.
Чтобы качественно выполнить сооружение конструкции, базовых основ может быть недостаточно, и придется протаптывать более тонкие пути направления. Модуль упругости стали – один из моментов, который пригодится инженерам проектирования.
Что именно из себя представляет термин, его расчеты в отношении стали и прочие нюансы вопроса будут рассмотрены далее.
Что такое модуль упругости стали: определение + назначение
Предположим, инженер производит сооружение массивной конструкции. Выбор материала крайне важен, ибо от результата принятого решения будет зависеть прочность всего проекта. Тип материала и сечение профиля выбирается на основании показателя модуля упругости. Задача человека – подобрать оптимальный размер элемента, параметры которого смогут сдержать статическую/динамическую нагрузку + не выгребут из кармана застройщика последние деньги.
1) Модуль упругости: что это такое?
В природе 100% физических тел имеют свойство менять форму при использовании на них силы давления. Вопрос в том, насколько сильно тело восстановит свою форму после изначальной деформации, и случится ли это вообще.
А) Терминология по модулю упругости
Давайте обратимся к повседневным объектам. Нажмите на буханку мягкого хлеба с качественной муки, и вы увидите близкое к полному восстановление формы. Другой пример – антистресс игрушка на основании полиуретана. Сжимайте ее, как пожелаете, за 30-60 секунд игрушка полностью вернет свою формы к изначальной. В сравнение, брусок пластилина считается полностью неупругим телом.
Важно: у каждого тела имеется точка невозврата деформации, когда приложенные усилия достигают своего предела. В таком случае искажается кристаллическая структура материала, и оно либо разрушается, либо остается в деформированной форме навсегда.
Впервые о модуле упругости завели речь еще в 17 веке. Труды шли от имени, известного в научных кругах физиков, ученого – Юнги. Помощником в разработке теории был Гук. Именно связка данных двух личностей привела к возникновению взаимосвязанных понятий – Закон Гука и модуль Юнга. Применяемость оговоренных законов крайне широка в инженерном деле, при определении прочности конструкции/изделия.
Модуль упругости стали (модуль Юнга) – характеристика металлического элемента. В основе меры лежит сопротивляемость деформации растяжения. По-простому, цифра дает понять на сколько металл перед глазами инженера пластичен.
Обозначается модуль Юнги через латинскую букву «Е». Единица измерения – ньютоны на метры в квадрате или Паскали. В инженерной практике больше устоялся именно второй вариант размерности. Для расчета модуля упругости используется обобщенная формула, которую можете лицезреть на рисунке ниже.
Физический смысл модуля упругости – напряжение, что вызывается при вытягивании исследуемого образца на длину, в два раза большую от первоначальной. В процессе эксперимента, предмет исследования обязан оставаться целым, но из-за сложности выполнения данного условия, модуль Юнга рассчитывают косвенным путем, через применение малых деформаций.
Б) Предел прочности и допускаемое механическое напряжение
Выделяют два типа предела прочности:
Для 85% веществ в природе значение динамического предела выше, нежели значение статического. Если классические гидравлические машины не в состоянии определить предел прочности образца металла или прочего вещества, на помощь приходят направленные взрывы в герметичной капсуле.
Различные вещества имеют свои особенности сопротивления деформациям. Для твёрдых тел важную роль отыгрывает прочность межатомных связей. При усилиях в сторону растяжения, расстояние между атомами внутри стали и других веществ увеличивается. Пропорционально возрастает и сопротивление прилагаемым усилиям.
Обратите внимание: существует так называемая теоретическая прочность стали – 1/10 от модуля упругости тестируемого вещества. Актуально для всех твердых веществ на основе железа. При достижении оговоренного значения, межатомные связи начинают разрушаться.
В реальных условиях сталь имеет неоднородную структуру, из-за чего разрывы распределяются по всей длине элемента неравномерно. Первым рушатся те участки, где межатомное напряжение выше всего.
В связи с оговоренным выше, в строительстве введено такое понятие как «запас прочности». То бишь, если человек занимается производством стальных тросов, он обязан вкладывать по ГОСТу не менее десятикратного запаса прочности от максимально допустимого теоретического предела. Если речь идет о каркасе здания, необходимо закладывать еще больший запас прочности от минимального.
Все расчеты по запасу прочности в промышленных масштабах производятся на специализированном оборудовании при использовании сложных математических формул. Для домашнего просчета имеются более доступные способы расчета показателей. К примеру, онлайн-калькуляторы инженерного типа.
В) Связь модуля упругости с другими физическими величинами
Выделяют и менее значимые показатели деформации объектов. Пример таких — параметры Ламе, которые являются константами материального типа, отображающие характеристики по упругим деформациям твердых тел. Кроме того, существуют изотропные и анизотропные материалы. Первые меняют механические свойства в зависимости от прилагаемой нагрузки, а вторые остаются неизменными. Сталь и прочие металлические сплавы относятся к изотропным материалам.
2) Пару слов о стали
Важно: рост доли углерода в сплаве стали приводит к повышению характеристик прочности материала в строительстве, но у данного момента имеется и отрицательная сторона – снижение пластичности (сталь становится хрупкой) и меньшая восприимчивость к сварочным работам.
Обращаясь к практической стороне вопроса, среднее содержание углерода в 85%+ марок стали находится в пределах 1% (колебания в пару десятых). В зависимости от вспомогательных добавок цветных металлов и прочих веществ, вхождение чистого железа может падать до 45% от общего объема.
Добавки в промышленности именуются легирующими компонентами, и чем больше их имеет сталь, тем сильнее меняются физические/химические свойства материала.
Картинка выше отображает распространенные маркировки конструкционных типов стали в зависимости от количества добавок в сплаве и соответствию ГОСТам. В основе маркировки лежит один из двух признаков – химический состав сплава или перечисление уровней базовых свойств. По территории нашего государства большее распространение приобрела именно первая разновидность классификации.
Базовые показатели стальных сплавов:
В зависимости от количества вредных примесей в стальном сплаве, те классифицируют по степени чистоты на обыкновенно качественные, качественные, высококачественные и особовысококачественные. Основными «вредными» добавками здесь выступают фосфор и сера. Детальнее о классификациях марок стали по их свойствам, методам изготовления и прочим параметрам можно прочитать в ГОСТах РФ.
Разъяснение понятия о модуле упругости, как физической величине:
Как посчитать модуль упругости стали?
Важно понимать, что модуль упругости Юнга не относится к постоянным величинам. Даже одна и та же марка стали может менять значения в зависимости от точечного применения силы на предмет (колебания незначительные, но они все же есть). Если говорить о более-менее точных показателях, то ими в мире металлов может похвастаться только алюминий, сталь и медь.
Пример выше для строительных материалов взят из справочника, но цифры на бумаге не всегда отображают на 100% верные данные. Куда правильнее будет обратиться к онлайн-расчётам, или воспользоваться специализированным софтом.
Как узнать модуль упругости стали:
Здесь же можно прочесть условные обозначения. Все физические характеристики материалов приняты по ПНАЭ Г-7-002-86, а промежуточные значения расчетных данных модуля упругости стали определяются методом линейной интерполяции.
Перед непосредственным использованием полученной информации на практике, следует провести сверку с ГОСТами. Неофициальные источники информации могут использоваться лишь для прикидочных расчетов и домашнем строительстве.
При возведении масштабных объектов, модуль Юнга нужно проверять по несколько раз, ведь от выбранных элементов будет зависеть крепость конструкции в целом.
Показатель предела нагрузки на сталь — модуль упругости Юнга
Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.
Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.
Модуль упругости — что это?
Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.
Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:
Модуль Юнга (упругости)
Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Таблица показателей упругости материалов
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.
Модуль упругости различных материалов
Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.
После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.
Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:
Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.
Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).
Значения модуля юнга для некоторых материалов
В таблице показаны значения E ряда распространенных веществ.
| Материал | модуль Юнга E, ГПа |
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Графен | 1000 |
| Латунь | 95 |
| Лёд | 3 |
| Медь | 110 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 200/210 |
| Стекло | 70 |
Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Общие понятия
Модуль упругости (модуль Юнга) — это показатель механического свойства материала, характеризующий его сопротивляемость деформации растяжения. Иными словами, это значение пластичности материала. Чем выше значения модуля упругости, тем меньше будет какой-либо стержень растягиваться при иных равных нагрузках (площадь сечения, величина нагрузки и другие).
Модуль Юнга в теории упругости обозначается буквой Е. Он является составляющей закона Гука (о деформации упругих тел). Эта величина связывает возникающее в образце напряжение и его деформацию.
Измеряется эта величина согласно стандартной международной системе единиц в МПа (Мегапаскалях). Но инженеры на практике больше склоняются к применению размерности кгс/см2.
Опытным путём осуществляется определение этого показателя в научных лабораториях. Сутью этого метода является разрыв гантелеобразных образцов материала на специальном оборудовании. Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости.
Таким образом определяется только модуль Юнга материалов упругих: медь, сталь и прочее. А материалы хрупкие сжимают до того момента, пока не появятся трещины: бетон, чугун и им подобные.
Растяжение.
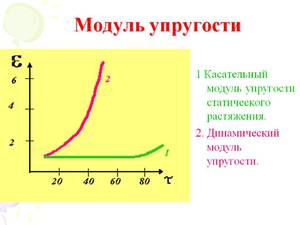
Соотношение между напряжением и деформацией для материалов часто исследуют, проводя испытания на растяжение, и при этом получают диаграмму растяжения – график, по горизонтальной оси которого откладывается деформация, а по вертикальной – напряжение (рис. 1). Хотя при растяжении поперечное сечение образца уменьшается (а длина увеличивается), напряжение обычно вычисляют, относя силу к исходной площади поперечного сечения, а не к уменьшенной, которая давала бы истинное напряжение. При малых деформациях это не имеет особого значения, но при больших может приводить к заметной разнице. На рис. 1 представлены кривые деформация – напряжение для двух материалов с неодинаковой пластичностью. (Пластичность – это способность материала удлиняться без разрушения, но и без возврата к первоначальной форме после снятия нагрузки.) Начальный линейный участок как той, так и другой кривой заканчивается в точке предела текучести, где начинается пластическое течение. Для менее пластичного материала высшая точка диаграммы, его предел прочности на растяжение, соответствует разрушению. Для более пластичного материала предел прочности на растяжение достигается тогда, когда скорость уменьшения поперечного сечения при деформировании становится больше скорости деформационного упрочнения. На этой стадии в ходе испытания начинается образование «шейки» (локальное ускоренное уменьшение поперечного сечения). Хотя способность образца выдерживать нагрузку уменьшается, материал в шейке продолжает упрочняться. Испытание заканчивается разрывом шейки.
Типичные значения величин, характеризующих прочность на растяжение ряда металлов и сплавов, представлены в табл. 2. Нетрудно видеть, что эти значения для одного и того же материала могут сильно различаться в зависимости от обработки.
Таблица 2
| Таблица 2 | ||||
| Металлы и сплавы | Состояние | Предел текучести, МПа | Предел прочности на растяжение, МПа | Удлинение, % |
| Малоуглеродистая сталь (0,2% С) | Горячекатанная | 300 | 450 | 35 |
| Среднеуглеродистая сталь (0,4% С, 0,5% Mn) | Упрочненная и отпущенная | 450 | 700 | 21 |
| Высокопрочная сталь (0,4% С, 1,0% Mn, 1,5% Si, 2,0% Cr, 0,5% Мo) | Упрочненная и отпущенная | 1750 | 2300 | 11 |
| Серый чугун | После литья | – | 175–300 | 0,4 |
| Алюминий технически чистый | Отожженный | 35 | 90 | 45 |
| Алюминий технически чистый | Деформационно-упрочненный | 150 | 170 | 15 |
| Алюминиевый сплав (4,5% Cu, 1,5% Mg, 0,6% Mn) | Упрочненный старением | 360 | 500 | 13 |
| Латунь листовая (70% Cu, 30% Zn) | Полностью отожженная | 80 | 300 | 66 |
| Латунь листовая (70% Cu, 30% Zn) | Деформационно-упрочненная | 500 | 530 | 8 |
| Вольфрам, проволока | Тянутая до диаметра 0,63 мм | 2200 | 2300 | 2,5 |
| Свинец | После литья | 0,006 | 12 | 30 |
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.
Инструмент для определения предела прочности
Читать также: Чем отличается малярный шпатель от фасадного
Модуль деформации стали и её упругости
Основной главной задачей инженерного проектирования служит выбор оптимального сечения профиля и материала конструкции. Нужно найти именно тот размер, который обеспечит сохранение формы системы при минимальной возможной массе под влиянием нагрузки. К примеру, какую именно сталь следует применять в качестве пролётной балки сооружения? Материал может использоваться нерационально, усложнится монтаж и утяжелится конструкция, увеличатся финансовые затраты. На этот вопрос ответит такое понятие как модуль упругости стали. Он же позволит на самой ранней стадии избежать появления этих проблем.
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
Читать также: Как очистить клей момент от рук






















