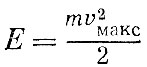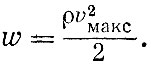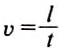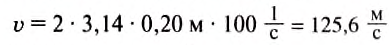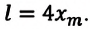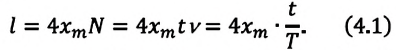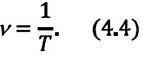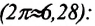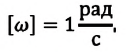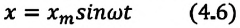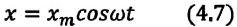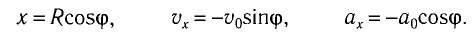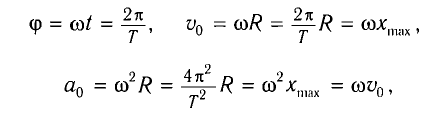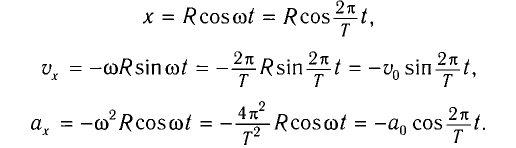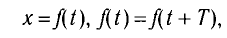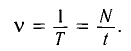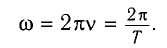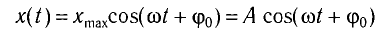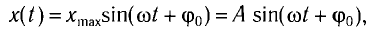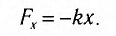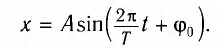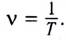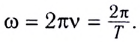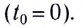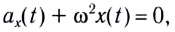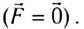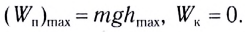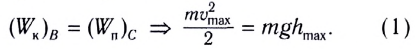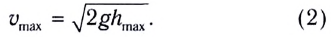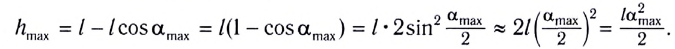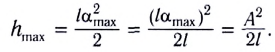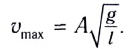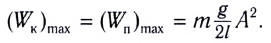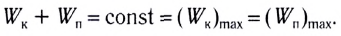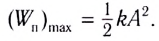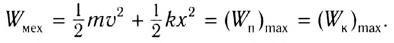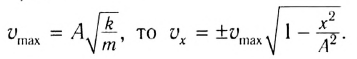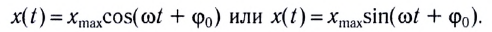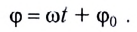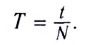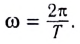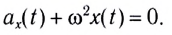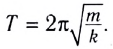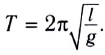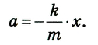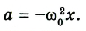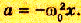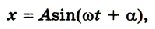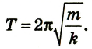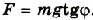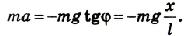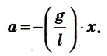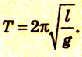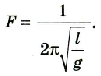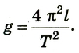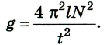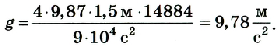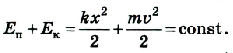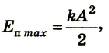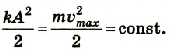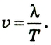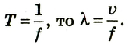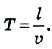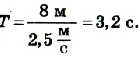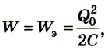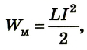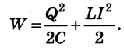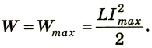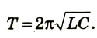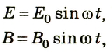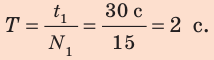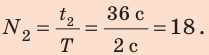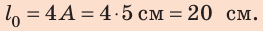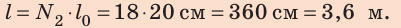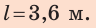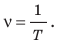чем выше амплитуда колебаний тем

Амплитуда, период, частота колебаний.

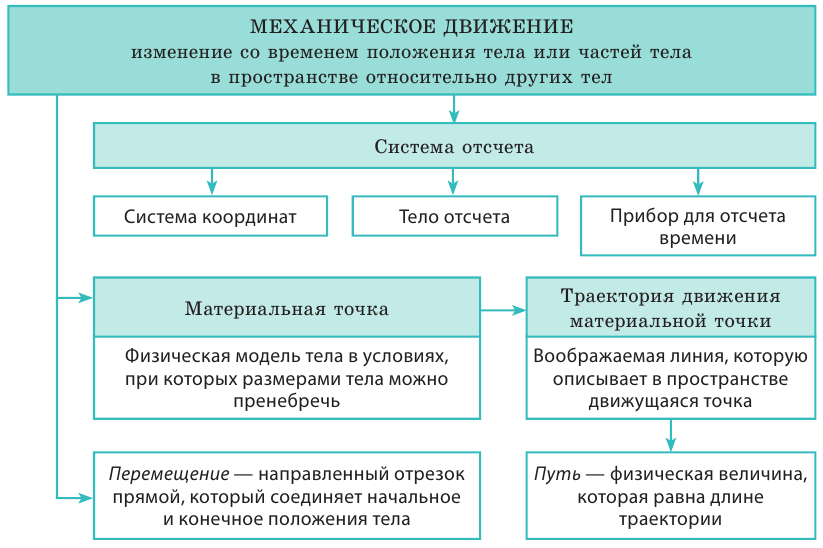
Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.

Для маятника это максимальное расстояние, на которое удаляется ша­рик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.

Амплитуда колебаний измеряется в единицах длины — метрах, санти­метрах и т. д. На графике колебаний амплитуда определяется как макси­мальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).

Период колебаний.

Период колебаний — это наименьший промежуток времени, через который система, соверша­ющая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.

Другими словами, период колебаний (Т) — это время, за которое совершается одно полное ко­лебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.

За полный период колебаний, таким образом, тело проходит путь, равный четы­рем амплитудам. Период колебаний измеряется в единицах времени — секундах, минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).

Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющей­ся величины точно повторяются через определенный промежуток времени, т. е. для гармоничес­ких колебаний. Однако это понятие применяется также и для случаев приблизительно повторяю­щихся величин, например, для затухающих колебаний.

Частота колебаний.

Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.

Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

.

В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:

.

Циклическая частота — это число колебаний, совершаемых за 2π секунд.

Источник

Чем выше амплитуда колебаний тем

195 дн. с момента
до конца учебного года

Источники звука. Звуковые колебания. Характеристики звука

Источники звука. Звуковые колебания

Человек живёт в мире звуков. Звук для человека является источником информации. Он предостерегает людей об опасности. Звук в виде музыки, пения птиц доставляет нам удовольствие. Нам приятно слушать человека с приятным голосом. Звуки важны не только для человека, но и для животных, которым хорошее улавливание звука помогает выжить.

Причина звука – вибрация (колебания) тел, хотя эти колебания зачастую незаметны для нашего глаза.

Если создать вакуум, то будем ли мы различать звуки? Роберт Бойль в 1660 году поместил часы в стеклянный сосуд. Откачав воздух, он не услышал звука. Опыт доказывает, что для распространения звука необходима среда.

Звук может также распространятся в жидкой и твердой среде. Под водой хорошо слышны удары камней. Положим часы на один конец деревянной доски. Приложив ухо к другому концу, можно ясно услышать тиканье часов.

Колебания с частотой меньше 16 Гц называется инфразвуком. Колебания с частотой больше 20000 Гц называются ультразвуком.

Звуковая волна (звуковые колебания) – это передающиеся в пространстве механические колебания молекул вещества (например, воздуха). Давайте представим себе, каким образом происходит распространение звуковых волн в пространстве. В результате каких-то возмущений (например, в результате колебаний диффузора громкоговорителя или гитарной струны), вызывающих движение и колебания воздуха в определенной точке пространства, возникает перепад давления в этом месте, так как воздух в процессе движения сжимается, в результате чего возникает избыточное давление, толкающее окружающие слои воздуха. Эти слои сжимаются, что в свою очередь снова создает избыточное давление, влияющее на соседние слои воздуха. Так, как бы по цепочке, происходит передача первоначального возмущения в пространстве из одной точки в другую. Этот процесс описывает механизм распространения в пространстве звуковой волны. Тело, создающее возмущение (колебания) воздуха, называют источником звука.

Привычное для всех нас понятие «звук» означает всего лишь воспринимаемый слуховым аппаратом человека набор звуковых колебаний. О том, какие колебания человек воспринимает, а какие нет, мы поговорим позднее.

Звуковые колебания, а также вообще все колебания, как известно из физики, характеризуются амплитудой (интенсивностью), частотой и фазой.

Приложив ухо к рельсам, можно услышать шум приближающегося поезда значительно раньше и на большем расстоянии. Значит металл проводит звук быстрее и лучше, чем воздух. Вода тоже хорошо проводит звук. Нырнув в воду, можно отчетливо слышать, как стучат друг о друга камни, как шумит во время прибоя галька.

Свойство воды – хорошо проводить звук – широко используется для разведки в море во время войны, а также для измерения морских глубин.

Необходимое условие распространения звуковых волн – наличие материальной среды. В вакууме звуковые волны не распространяются, так как там нет частиц, передающих взаимодействие от источника колебаний.

Поэтому на Луне из-за отсутствия атмосферы царит полная тишина. Даже падение метеорита на ее поверхность не слышно наблюдателю.

В отношении звуковых волн очень важно упомянуть такую характеристику, как скорость распространения.

В каждой среде звук распространяется с разной скоростью.

Скорость звука в воде — 1500 м/с.

Скорость звука в металлах, в стали — 5000 м/с.

В теплом воздухе скорость звука больше, чем в холодном, что приводит к изменению направления распространения звука.

Высота, тембр и громкость звука

Звуки бывают разными. Для характеристики звука вводят специальные величины: громкость, высота и тембр звука.

Громкость звука зависит от амплитуды колебаний: чем больше амплитуда колебаний, тем громче звук. Кроме того, восприятие громкости звука нашим ухом зависит от частоты колебаний в звуковой волне. Более высокочастотные волны воспринимаются как более громкие.

За единицу громкости звука принят 1 Бел (в честь Александра Грэхема Белла, изобретателя телефона). Громкость звука равна 1 Б, если его мощность в 10 раз больше порога слышимости.

На практике громкость измеряют в децибелах (дБ).

1 дБ = 0,1Б. 10 дБ – шепот; 20–30 дБ – норма шума в жилых помещениях;

50 дБ – разговор средней громкости;

70 дБ – шум пишущей машинки;

80 дБ – шум работающего двигателя грузового автомобиля;

120 дБ – шум работающего трактора на расстоянии 1 м

130 дБ – порог болевого ощущения.

Звук громкостью свыше 180 дБ может даже вызвать разрыв барабанной перепонки.

Частота зв уковой волны определяет высоту тона. Чем больше частота колебаний источника звука, тем выше издаваемый им звук. Человеческие голоса по высоте делят на несколько диапазонов.

Согласно легенде, Пифаго р все музыкальные звуки расположил в ряд, разбив этот ряд на части – октавы, – а

октаву – на 12 частей (7 основных то нов и 5 полутонов). Всего насчитывается 10 октав, обычно при исполнении музыкальных произведений используются 7–8 октав. Звуки частотой более 3000 Гц в качестве музыкальных тонов не используются, они слишком резки и пронзительны.

Источник

Чем выше амплитуда колебаний тем

Звуковые колебания и волны

Речь идет о воздухе лишь потому, что звук чаще всего передается через воздух. Но, разумеется, нет никаких особых свойств у воздуха, чтобы за ним оказалось монопольное право совершать звуковые колебания. Звуковые колебания возникают в любой среде, способной сжиматься, а так как несжимающихся тел в природе нет, то, значит, частицы любого материала могут оказаться в этих условиях. Учение о таких колебаниях обычно называют акустикой.

При прохождении равновесного положений скорость колеблющейся частицы максимальна. Напротив, в положениях крайних смещений скорость частицы, естественно, равняется нулю. Мы уже говорили, что если смещение частицы подчиняется закону гармонического колебания, то и изменение скорости колебания следует тому же закону. Если обозначить амплитуду смещения через s₀, а амплитуду скорости через v₀, то v₀ = 2πs₀ /_T иди ν 0 = 2πvs₀. Громкий разговор приводит частицы воздуха в колебание с амплитудой смещения всего лишь в несколько миллионных долей сантиметра. Амплитудное значение скорости будет величиной порядка 0,02 см/с.

Струна, колеблющаяся по закону синуса, приводит и частицы воздуха в гармоническое колебание. Шумы и музыкальные аккорды приводят к значительно более сложной картине. На рис. 6.9 показана запись звуковых колебаний, а именно звукового давления в зависимости от времени. Эта кривая мало похожа на синусоиду. Оказывается, однако, что любое сколь угодно сложное колебание может быть представлено как результат наложения одной на другую большого числа синусоид с разными амплитудами и частотами. Эти простые колебания, как говорят, составляют спектр сложного колебания. Для простого примера такое сложение колебаний показано на рис. 6.10.

Если бы звук распространялся мгновенно, то все частицы воздуха колебались бы, как одна. Но звук распространяется не мгновенно, и объемы воздуха, лежащие на линии распространения, приходят в движение по очереди, как бы подхватываются волной, идущей от источника. Так же точно щепка лежит спокойно на воде до тех пор, пока круговые водяные волны от брошенного камешка не подхватят ее и не приведут в колебание.

Через промежутки λ мы будем встречать колеблющиеся в такт точки. Точки, находящиеся на расстоянии λ /₂, будут совершать движение одна по отношению к другой, как предмет, колеблющийся перпендикулярно к зеркалу, по отношению к своему изображению.

Если изобразить смещение (или скорость, или звуковое давление) всех точек, лежащих на линии распространения гармонического звука, то получится опять синусоида.

На рисунке звуковой волны смещения частицы отложены по вертикали, а направлением распространения волны, вдоль которого отсчитывается расстояние, является горизонталь. Это может навести на неверную мысль, что частицы смещаются перпендикулярно к направлению распространения волны. В действительности частицы воздуха всегда колеблются вдоль направления распространения звука. Такая волна называется продольной.

Свет распространяется несравненно быстрее, чем звук,- практически мгновенно. Гром и молния происходят в один и тот же момент, но молнию мы видим в момент ее возникновения, а звук грома доходит до нас со скоростью примерно один километр за три секунды (скорость звука в воздухе составляет 330 м /_с). Значит когда слышен гром, опасность удара молнии уже миновала.

Зная скорость распространения звука, обычно можно определить, как далеко проходит гроза. Если от момента вспышки молнии до раската грома прошло 12 с, значит, гроза от нас за 4 км.

Направляя звук не вниз, а вперед или в стороны, можно при его помощи определить, нет ли около корабля опасных подводных скал или глубоко погруженных в воду айсбергов. Все частицы воздуха, окружающего звучащее тело, находятся в состоянии колебания. Как мы выяснили в книге 1, колеблющаяся по закону синуса материальная точка обладает определенной и неизменной полной энергией.

Когда колеблющаяся точка проходит положение равновесия, скорость ее максимальна. Так как смещенные точки в это мгновение равняется нулю, то вся энергия сводится к кинетической:

Следовательно, полная энергия пропорциональна квадрату амплитудного значения скорости колебания.

Так как масса единицы объема есть плотность ρ, то плотность звуковой энергии

Амплитуда скорости звукового колебания при громком разговоре равняется 0,02 см /_с. 1 см 3 воздуха весит около 0,001 г. Таким образом, плотность энергии равняется

При громком разговоре интенсивность звука вблизи собеседников будет примерно равна (мы воспользуемся числом, полученным выше)

Источник

Механические колебания.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Гармонические колебания.

Выясним смысл входящих в эту формулу величин.

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1) :

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Рис. 2. Закон косинуса

Рис. 3. Закон синуса

Уравнение гармонических колебаний.

Теперь дифференцируем полученное равенство (4) :

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Пружинный маятник.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4 ). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

Тогда соотношение (8) принимает вид:

Циклическая частота колебаний пружинного маятника, таким образом, равна:

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

Математический маятник.

Рис. 5. Математический маятник

Запишем для маятника второй закон Ньютона:

и спроектируем его на ось :

Если маятник занимает положение как на рисунке (т. е. 0′ alt=’x>0′ /> ), то:

Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:

Итак, при любом положении маятника имеем:

Следовательно, циклическая частота колебаний математического маятника равна:

Отсюда период колебаний математического маятника:

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6 ).

Рис. 6. Затухающие колебания

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Рис. 7. Резонанс

Источник

Содержание:

Колебательное движение:

Колебательное движение (колебания) — один из наиболее распространённых процессов в природе и технике.

Наблюдение. Под действием ветра колеблются высотные дома и высоковольтные линии электропередачи, совершают колебания маятник заведённых часов, автомобиль на рессорах во время движения. Землетрясения — это колебания земной коры, приливы и отливы — колебания уровня воды в морях и океанах, обусловленные притяжением Луны, удары пульса — результат периодических сокращений сердечной мышцы человека.

Колебательные явления изучает специальный раздел физики — теория колебаний. Знания о колебательных процессах нужны судо- и самолётостроителям, специалистам промышленности и транспорта, конструкторам радиотехнической и звуковой аппаратуры и др.

Опыт 1.

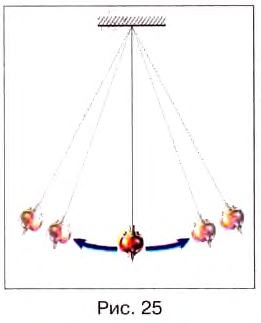
Для наблюдения и изучения колебаний, а также для применения в разнообразных приборах используют маятники. Простейший маятник — это шарик, подвешенный на нити к какой-либо опоре. Если шарик отклонить от исходного положения равновесия и отпустить, то он начнёт двигаться слева направо, справа налево до тех пор, пока колебания не прекратятся (рис. 25).

В физике маятник подобной конструкции называют математическим маятником.

Каковы же самые характерные признаки колебательных движении? Проведённый опыт даёт возможность сделать вывод, что во время колебаний определённые состояния движения тела повторяются или почти повторяется. Сделав одно полное колебание, т. е. пройдя путь от крайнего левого положения к крайнему правому и назад, тело, подвешенное на нити, и в дальнейшем будет повторять такое же движение. Мы уже знаем, если движение тела повторяется со временем, то его называют периодическим.

Повторяются движения поршня в двигателе автомобиля, лодок на волнах, стержня отбойного молотка, сита сортировочной установки. Всё это примеры механических колебаний.

Математический маятник состоит из нескольких тел, взаимодействующих между собой: Земля и шарик, шарик и нить, нить и опора в точке подвеса. Если действием других тел на маятник можно пренебречь, то говорят, что тела в составе маятника образуют колебательную систему. Если вывести колебательную систему из состояния равновесия — отклонить шарик из исходного положения и отпустить, то далее колебания будут продолжаться без внешнего вмешательства за счёт взаимодействия между телами системы. Колебания, происходящие в колебательной системе за счёт взаимно действия между образующими её телами, называют свободными.

Рассмотренные нами колебания шарика на нити являются примером свободных колебаний.

А какой вид имеют колебания и какими физическими величинами они характеризуются?

Опыт 2.

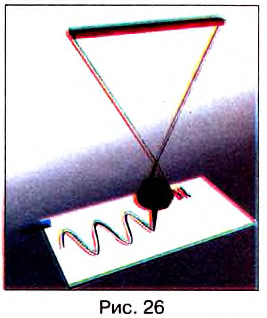
Возьмём маятник, в котором вместо шарика подвешен грузик со сквозным отверстием. С помощью такого устройства можно записывать колебания (рис. 26).

Установим в отверстие грузика фломастер, выведем грузик из положения равновесия и отпустим. Маятник колеблется, а фломастер, касаясь листа картона, который мы равномерно протягиваем во время колебаний, оставляет на нём след.

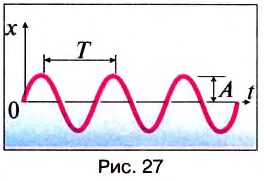
В результате опыта получаем график колебаний маятника в виде начерченной линии (рис. 27), т. е. зависимость отклонения маятника от времени. Позже будем подробно изучать эту важную волнистую линию, называемую синусоидой.

Как видно из рисунка 27, маятник в определенный момент отклоняется от положения равновесия на некоторое максимальное расстояние. Это отклонение маятника назвали амплитудой колебаний.

Амплитуду колебаний обозначают большой латинской буквой А. Её единицей в СИ является один метр (1 м). Значение амплитуды зависит только от того, на какое расстояние тело было отведено от положения равновесия до начала колебаний.

Маятник выполняет одно полное колебание за определённое время. Продолжительность одного полного колебания называют периодом колебаний.

Период колебаний обозначают большой латинской буквой Т. Его единицей в СИ является одна секунда (1 с).

Если за время t произошло N полных колебаний, то, чтобы определить период Т, нужно t поделить на N, т. е.: .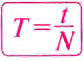

Опыт 3.

Возьмём маятник, как в опыте 2, но подвесим грузик на нить большей длины. Потом так же запишем график колебаний нового маятника и сравним его с (графиком в опыте 2. Увидим, что чем больше длина маятника, тем больше период его колебаний (рис. 28).

Период колебаний маятника зависит от его длины. Чем длиннее маятник, тем больше период его колебаний.

Если выполнить опыты с пружинным маятником, который состоит из пружины и подвешенного к нему тела, то окажется, что чем больше масса подвешенного к пружине тела, тем больше период колебаний пружинного маятника.

Колебания характеризуются также частотой колебаний, которая обозначается греческой буквой 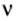(ню).

Частота колебаний определяется числом колебаний, выполненных системой за единицу времени.

Частота и период колебаний связаны обратно пропорциональной зависимостью, поэтому: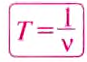
,

где Т— период колебаний; — частота колебаний.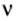

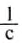
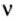
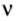
Единицей частоты в СИ является один герц (1 Гц). 1 Гц = 1 . Она названа так в честь известного немецкого физика Генриха Герца. Если частота колебаний = 1 Гц, то это означает, что происходит одно колебание в секунду. Приблизительно с такой частотой бьётся человеческое сердце. Если = 50 Гц, то происходят 50 колебаний в секунду.

Пример задачи:

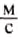
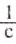
Если при вращении шлифовального круга скорость движения точек на его краю равна 95 , то возникает опасность разрыва круга. Можно ли этот круг радиусом 20 см вращать с частотой 100 ?

Дано:

= 95

= 20см

= 100

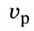
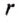
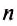
Решение:

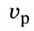
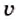
По условию задачи — значение скорости, при которой возникает опасность разрыва круга; — значение скорости, которую будут иметь точки на краю круга, определяем по формуле

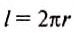
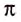
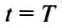
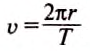
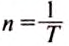
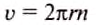
Для одного оборота путь , где = 3,14;

, а , тогда .

Подставив значения, получим:

Ответ: полученное значение скорости больше того, при котором возникает опасность разрыва. Значит, шлифовальный круг нельзя вращать с частотой 100 .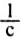

На первый взгляд, приведенные примеры колебаний имеют мало общего. Однако при их исследовании выяснилось, что разные по природе колебания описываются одинаковыми математическими уравнениями, что значительно облегчает их изучение.

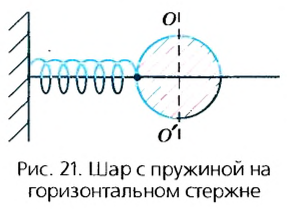
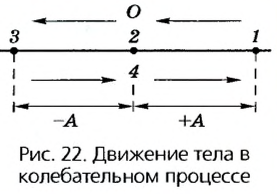
Переместим шар вправо от положения равновесия, пружина при I этом растянется. Если шар отпустить, пружина заставит его двигаться к положению равновесия. Поскольку в системе трения нет, то шар пройдет положение равновесия и, двигаясь влево, сожмет пружину. Достигнув крайнего левого положения, шар будет двигаться вправо и вернется в крайнее правое положение. Пружина при этом опять будет максимально растянутой. В данном случае шар выполнит одно полное колебание. В дальнейшем в идеальной системе (без трения) такие колебания будут совершаться как угодно долго.

Очевидно, что отличительной особенностью колебаний является их периодичность. Но периодичными являются и вращательные движения. В отличие от вращательных движений, у которых для каждой точки имеются траектории в виде окружности, во время колебательных движений точка или тело двигаются в противоположных направлениях по одной и той же траектории.

На рисунке 22 изображено одно полное колебание шара с пружиной. Движение осуществляется в такой последовательности от точки к точке:

и опять повторяется.

Максимальное отклонение колеблющегося тела от положения равновесия называется амплитудой колебания тела (на рис. +А и -А).

Время, в течение которого осуществляется одно полное колебание тела, называется периодом колебания тела Т.

Основной единицей периода колебаний является секунда.

Частота колебаний измеряется в единицах в секунду. Эта единица Частота колебаний называется герц (Гц) в честь немецкого физика Генриха Герца, который в 1884 г. экспериментально доказал существование электромагнитных волн.

Частота колебаний f* показывает какое количество колебаний совершает тело за единицу времени.

Период колебания тел Т связан с частотой их колебаний f соотношением:

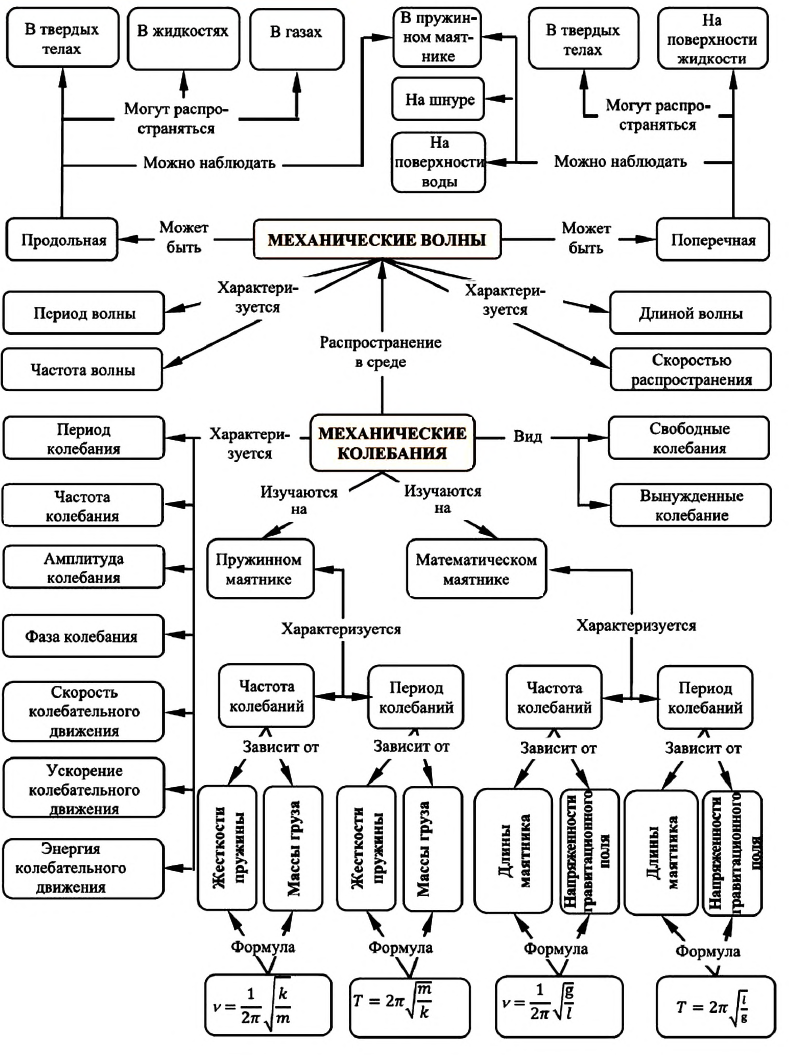
Карта колебательного движения

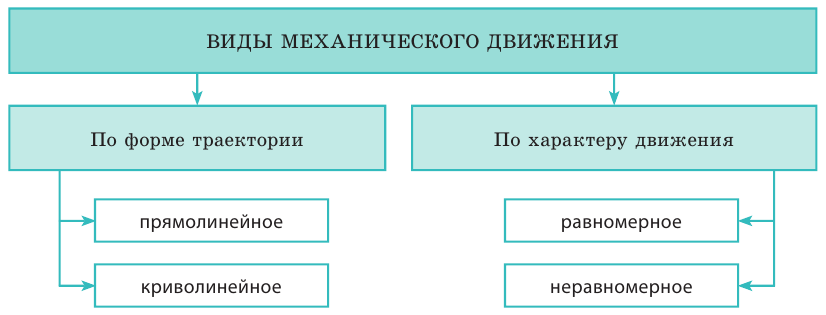
Колебательное движение может быть периодическим и непериодическим:

Периодическое колебательное движение — это колебания тела или системы тел, повторяющиеся через одинаковые промежутки времени.

Непериодическое колебательное движение — это колебания тела или системы тел, повторяющиеся через произвольные промежутки времени. У таких колебаний определенных периодов нет.

Периодические колебания в основном бывают двух видов: вынужденные и свободные колебания.

Вынужденные колебания — это колебания, возникающие в результате воздействия внешней периодически изменяющейся силы.

Свободные колебания — это колебания, возникающие в результате действия внутренних сил замкнутой системы.

Свободные колебания:

Для простоты проведения измерений и вычислений при изучении колебательного движения удобно воспользоваться замкнутой системой. В замкнутой системе тела совершают колебательные движения в результате действия внутренних сил.

Кинематические характеристики колебательного движения. Ознакомимся с некоторыми из них.

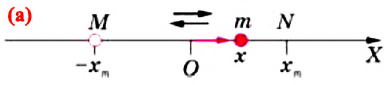
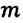
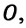
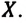
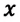
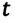
Смещение — это физическая величина, показывающая, в какую сторону и на сколько удаляется от положения равновесия колеблющееся тело за определенный промежуток времени. Например, предположим, что тело массой совершает повторяющиеся периодические движения вокруг точки равновесия вправо и влево от нее, вдоль оси Координата тела в данный момент времени показывает смещение этого тела от его положения равновесия (а).

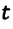
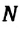
Если тело за промежуток времени совершит колебаний, то пройденный им путь будет равен:

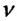
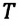
Где (ню) — частота колебаний, — период колебаний.

Период и частота колебаний — взаимно обратные величины:

или

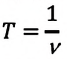
Циклическая частота, являясь величиной в 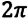раза большей частоты колебаний, показывает, сколько колебаний совершает тело за 6,28 секунды

Здесь 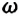(омега) — циклическая частота. Единица измерения циклической частоты в СИ:

Гармоническое колебание и его график:

Самым простым колебательным движением является гармоническое колебание.

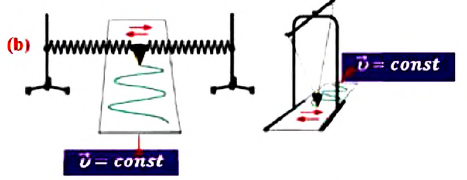
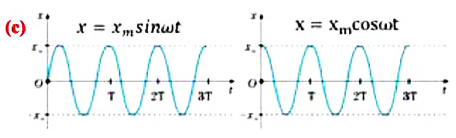
Изменения положения тела, совершающего свободные гармонические колебания, описываются кривой, которая является синусоидой или косинусоидой. Кривую синусоиды (или косинусоиды) с легкостью можно наблюдать во время проведения опыта как с пружинным, так и с нитевым маятником, представляющим собой наполненную песком воронку с небольшим отверстием внизу (b).

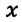
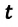
Эта кривая соответствует графику изменения перемещения маятника от времени по закону синуса или косинуса (с):

Из графика видно, что за время, равное периоду колебания маятник совершает одно полное колебание (см: с).

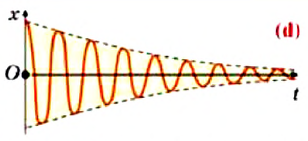
Отсутствие действия внешних сил на замкнутую систему приводит к тому, что ее полная механическая энергия не изменяется. Это означает, что в идеальных условиях амплитуда свободных колебаний в замкнутой системе не изменяется, то есть колебания не затухают. Однако в реальности свободные колебания затухают — под действием сил трения с течением времени полная механическая энергия системы уменьшается, то есть уменьшается амплитуда колебаний и колебания затухают (d).

Всё о колебательном движение

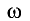
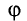
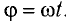
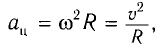
При равномерном вращении материальной точки по окружности радиусом R с угловой скоростью угол поворотаматериальной точки изменяется со временем по закону . При таком движении центростремительное (нормальное) ускорение материальной точки направлено к центру окружности и вычисляется по формуле где v — модуль линейной скорости.

Положение механической системы, в котором равнодействующая всех действующих сил равна нулю, называется положением равновесия.

Колебательным движением (колебаниями) называют всякий процесс, который обладает свойством повторяемости во времени. Периодическим называется движение, при котором физические величины, характеризующие его, через равные промежутки времени принимают одни и те же значения. Периодическое движение называется колебательным, если тело или материальная точка движется вблизи устойчивого положения равновесия, отклоняясь то в одну, то в другую сторону. При этом через любую точку траектории, за исключением крайних, тело проходит как в прямом, так и в обратном направлении. Следовательно, отличительным признаком колебательного движения является его возвратность.

Например, механическим колебательным движением является движение тела, подвешенного на нити, движение груза на пружине. Колебания могут быть не только механическими, но и электромагнитными (периодические изменения напряжения и силы тока в цепи), термодинамическими (колебания температуры с течением времени).

Таким образом, колебания — это особая форма движения. Его особенностью является тот факт, что различные по своей природе физические процессы (механические, электромагнитные и т. д.) описываются одинаковыми математическими зависимостями физических величин от времени.

Опыт показывает, что для возникновения и существования механических колебаний в некоторой системе необходимо выполнение определенных условий. Прежде всего, при выведении (например, при малом смещении) тела из положения равновесия в системе должна возникать результирующая сила, стремящаяся возвратить тело в положение равновесия. Кроме того, в системе должно существовать достаточно малое трение, поскольку в противном случае колебания быстро затухнут или могут не возникнуть вообще.

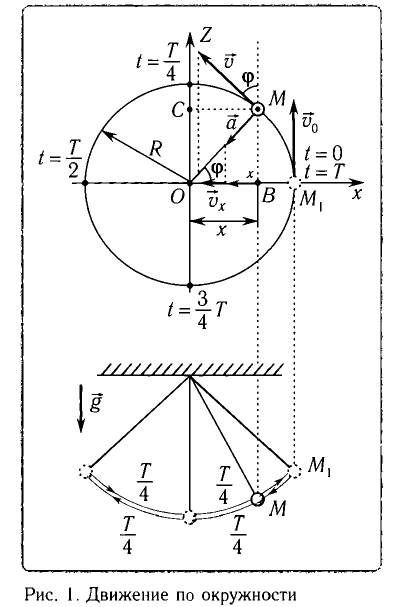
Рассмотрим движение небольшого тела М, которое будем считать материальной точкой (рис. 1), по окружности радиусом R с постоянной по модулю линейной скоростью 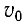. Пусть рассматриваемое движение происходит против хода часовой стрелки.

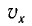
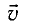
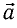
Соответственно, проекция линейной скорости материальной точки на ось Ох в данный момент времени является скоростью точки В, а проекция а, ее центростремительного ускорения — ускорением точки В.

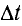
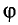
Радиус, соединяющий движущуюся точку М с центром окружности О, за промежуток времени повернулся на угол , называемый фазовым углом или просто фазой. Из рисунка видно, что

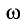
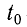
Если — угловая скорость движения материальной точки, а начальный момент движения = 0, то

где Т — период ее вращения по окружности.

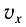
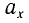
Тогда координату x, проекцию скорости и проекцию ускорения точки В в любой момент времени можно определить по формулам:

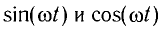
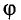
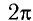
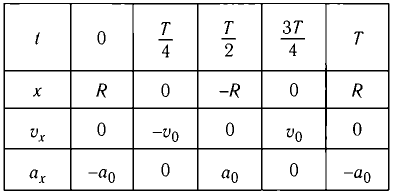
Поскольку функции периодические, то через промежуток времени Т, по истечении которого угол изменится на , все характеристики движения точки В вдоль оси Ох (координата, проекция скорости и проекция ускорения) примут прежние значения (табл. 1). Точка В в течение этого промежутка времени дважды проходит через центр окружности, двигаясь в противоположных направлениях вдоль оси Ох (см. рис. 1). Как уже отмечалось, возвратность — основной признак колебательного движения.

Таблица I

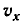
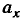
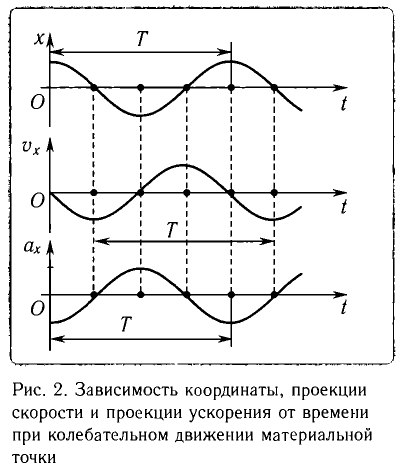
Координата х, проекция скорости и проекция ускорения тела, движущегося по окружности, в различные моменты времени t

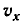
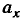
Зависимость координаты х, проекции скорости и проекции ускорения от времени t (промежутка времени) показаны на рисунке 2.

Наиболее важными величинами, характеризующими механические колебания, являются:

x(t) — координата материальной точки или ее отклонение из положения равновесия в момент времени t:

гдe f(t) — заданная периодическая функция времени t,T— период этой функции;

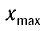
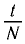
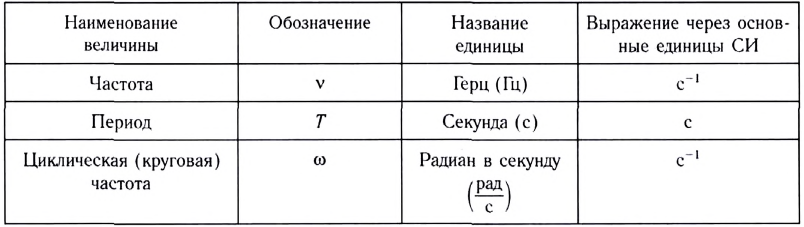
А (А > 0) — амплитуда — максимальное смещение тела или системы тел из положения устойчивого равновесия;

т = — период — длительность одного полного колебания, т. е. наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание. Здесь t — время совершения N полных колебаний.

В СИ основной единицей периода (времени) является секунда (1 с).

v — частота — число полных колебаний, совершаемых в единицу времени:

В СИ основной единицей частоты является герц (1 Гц). 1 Гц равен частоте, при которой за 1 с тело совершает одно полное колебание (1 Гц= 1 ).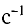

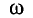
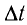
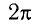
— циклическая частота — число полных колебаний, совершаемых за промежуток времени , равный секунд:

В СИ основной единицей циклической частоты является радиан в секунду (1)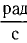

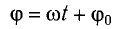
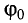
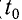
— фаза — аргумент периодической функции, определяющий значение физической величины в любой момент времени t. Она определяет состояние колебательной системы (координаты, скорости, ускорения) в любой момент времени при заданной амплитуде. Единицей фазы является радиан (1 рад).

— начальная фаза, определяющая состояние колебательной системы в начальный момент времени ( = 0).

Колебания, при которых координата (смещение) тела со временем изменяется по закону косинуса

называются гармоническими.

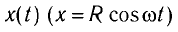
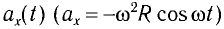
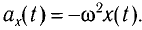
Обратим внимание на то, что координата и проекция ускорения точки В (см. рис. 1) в любой момент времени связаны соотношением. Это соотношение позволяет сделать вывод, что при гармонических колебаниях проекция ускорения точки прямо пропорциональна ее смещению от положения равновесия и противоположна ему по знаку.

Данное соотношение, записанное в виде

(1)

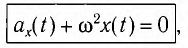
представляет собой уравнение гармонических колебаний (гармонического осциллятора).

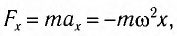
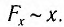
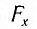
Так как ускорение всегда обусловлено действием силы, то т. е. При гармонических колебаниях проекция силы, возвращающей тело в положение равновесия (х = 0), пропорциональна его координате:

Знак «минус» отражает возвратный характер возникающей силы. Как уже отмечалось, появление возвращающей силы при отклонении тела от положения равновесия является необходимым условием возникновения колебаний.

При достаточно малой амплитуде любые колебания можно приближенно считать гармоническими.

Положению равновесия тела соответствует точка х = 0, так как при этом равнодействующая сила, приложенная к нему, равна нулю ().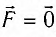

Различают несколько видов равновесия. Равновесие называется устойчивым, если при малом отклонении тела от положения равновесия возникают силы, возвращающие его в исходное положение. Равновесие называется неустойчивым, если при малом отклонении тела от положения равновесия возникают силы, вызывающие дальнейшее отклонение тела от положения равновесия. Равновесие называется безразличным, если при отклонении тела от положения равновесия равнодействующая сила остается равной нулю.

Примером устойчивого равновесия может служить равновесие небольшого шарика в сферической ямке, а примером неустойчивого — равновесие шарика на вершине сферической горки. Равновесие шарика на горизонтальной поверхности является безразличным.

Таким образом, колебания материальной точки являются гармоническими, если они происходят под действием возвращающей силы, модуль которой прямо пропорционален смещению точки из положения равновесия и направленной к положению равновесия колеблющегося тела.

Если рассмотреть проекцию точки М на ось Оу (точка С на рис. 1), то ее координата y(t) будет совершать гармонические колебания вдоль оси Оу.

Таким образом, движение по окружности с постоянной по модулю линейной скоростью можно рассматривать как два гармонических колебательных движения, происходящих одновременно в двух взаимно перпендикулярных направлениях.

Пример №1

За какую часть периода тело, совершающее гармонические колебания, проходит расстояние: а) от среднего положения до крайнего; б) первую половину этого расстояния; в) вторую половину этого расстояния?

Решение

Координата х тела, совершающего гармонические колебания, определяется

Здесь А — амплитуда, t — время, отсчитываемое с момента прохождения телом положения равновесия, Т — период колебаний, 0) — амплитуда — максимальное смещение 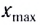тела или системы тел из положения равновесия;

Т — период — длительность одного полного колебания, т. е. наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание. В СИ единицей периода является секунда (1с);
v — частота — число полных колебаний в единицу времени:

В СИ единицей частоты колебаний является герц. Один герц равен частоте колебаний тела, при которой за одну секунду тело совершает одно полное колебание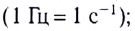
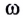
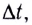
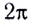
— циклическая частота — число полных колебаний за промежуток времени равный секунд:

В СИ единицей циклической частоты является радиан в секунду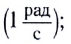
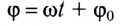
— фаза — аргумент периодической функции, определяющий значение изменяющейся физической величины в данный момент времени /.

Единицей фазы является радиан (1 рад);
— начальная фаза, определяющая положение тела в начальный момент времени

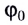
Колебания, при которых зависимость координаты (смещения) тела от времени описывается формулами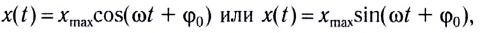

называются гармоническими.

Зависимость координаты от времени x(t) называется кинематическим законом гармонических колебаний (законом движения), поскольку позволяет определить положение тела, его скорость, ускорение в произвольный момент времени. Систему (тело), которая совершает гармонические колебания, называют гармонической колебательной системой или одномерным гармоническим осциллятором.

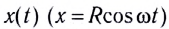
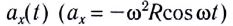
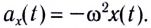
Обратим внимание на то, что координата и проекция ускорения точки В (см. рис. 180) в любой момент времени связаны соотношением Это соотношение позволяет сделать вывод, что при гармонических колебаниях проекция ускорения точки прямо пропорциональна ее смещению из положения равновесия и противоположна ему по знаку.

Данное соотношение, записанное в виде

представляет собой уравнение гармонических колебаний (гармонического осциллятора).

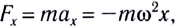
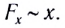
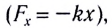
Так как ускорение всегда обусловлено действием силы, то т. е. При гармонических колебаниях модуль силы, возвращающей тело в положение равновесия (х = 0), пропорционален ее координате причем знак «минус» отражает «возвратный» характер возникающей силы. Как уже отмечалось, появление возвращающей силы при отклонении тела от положения равновесия является необходимым условием возникновения колебаний.

При достаточно малой амплитуде колебаний любой колебательный процесс можно приближенно считать гармоническим.
Положению равновесия соответствует точка х = 0, так как при этом сила, действующая на тело, равна нулю

Таким образом, колебания материальной точки являются гармоническими, если они происходят под действием возвращающей силы, модуль которой прямо пропорционален смещению точки из положения равновесия и направлен к положению равновесия колеблющегося тела.

Уравнение гармонических колебаний можно получить и с помощью законов динамики, анализируя силы, действующие на систему. Подобное (динамическое) описание не содержит никаких сведений ни об амплитуде, ни о начальной фазе. Его необходимо дополнять начальными условиями, а именно: задавать положение тела и его скорость в начальный момент времени.
Заметим, что гармонические колебания вдоль оси Оу будет совершать и координата у тела, вращающегося по окружности с постоянной по модулю скоростью (см. рис. 179).

Движение по окружности с постоянной по модулю скоростью можно рассматривать как два гармонических колебательных движения, совершаемых в двух взаимно перпендикулярных направлениях.

Превращения энергии при колебательном движении

Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.

Поскольку при одномерных колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.
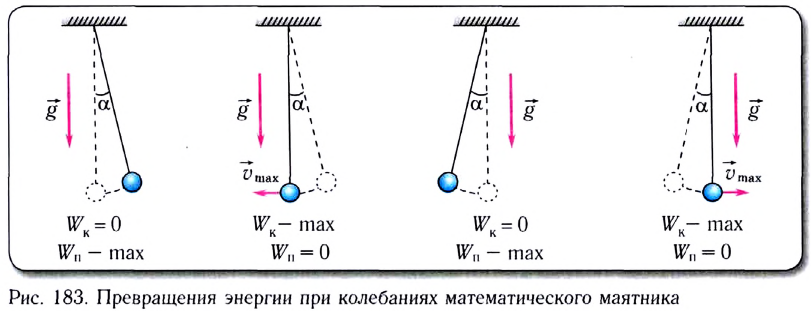
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.

При отклонении маятника на угол 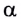(рис. 183), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:

Поскольку в положении равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:

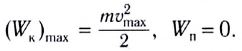
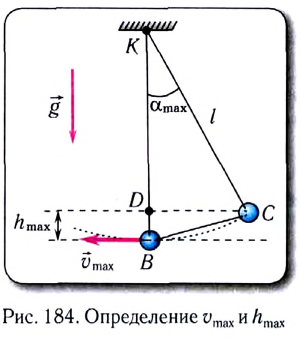
Из закона сохранения механической энергии следует (рис. 184), что

Отсюда найдем максимальную скорость маятника:

Высоту 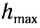можно выразить через длину маятника l и амплитуду колебаний А.

Если колебания малы, то 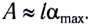Из треугольника KCD на рисунке 184 находим

Отсюда имеем

Подставив выражение для 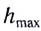в формулу (2), получим

Подставляя выражения для 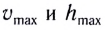в соотношение (1), находим

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.

В любом промежуточном положении

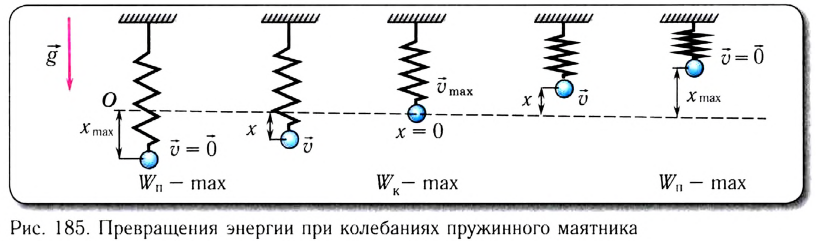
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 185).

В крайних точках, когда 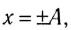скорость равна нулю (v = 0) и кинетическая энергия груза полностью переходит в потенциальную энергию деформированной пружины:

Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.

В положении равновесия, когда х = 0, вся энергия осциллятора переходит в кинетическую энергию груза: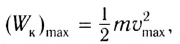

где 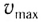— максимальная скорость при колебаниях.

В промежуточных точках полная энергия равна

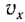
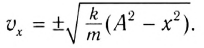
Отсюда можно вывести выражение для проекции скорости груза в точке с координатой х:

Так как максимальная скорость

Затухающие колебания. Вынужденные колебания. Резонанс

Как Вам уже известно, механическая энергия одномерного гармонического осциллятора пропорциональна квадрату амплитуды его колебаний. В любой реальной системе всегда присутствуют силы трения (сопротивления), поэтому механическая энергия системы с течением времени уменьшается, переходя во внутреннюю энергию. Вместе с тем убыль полной энергии означает и уменьшение амплитуды колебаний.

Колебания, происходящие с постоянной во времени амплитудой, называются незатухающими колебаниями.

Примерами таких колебаний служат колебания математического и пружинного маятников, происходящие в отсутствие сил трения.

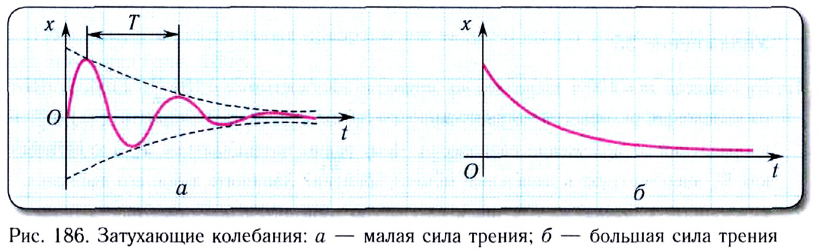
Колебания, амплитуда которых уменьшается с течением времени вследствие потери энергии колебательной системой, называются затухающими колебаниями (рис. 186, а, б).

Уменьшение механической энергии системы (превращение ее в теплоту) происходит вследствие трения и сопротивления окружающей среды. Такие системы называют диссипативными (от латинского слова dissipation — рассеяние).

При малых потерях энергии колебания можно считать периодическими и пользоваться такими понятиями, как период и частота колебаний. Так, например, период — промежуток времени между двумя последовательными максимумами колеблющейся физической величины (см. рис. 186, а).

Незатухающие колебания, вызванные кратковременным внешним возбуждением, называются свободными или собственными. Они происходят под действием внутренних сил, возникающих в самой системе. Собственные колебания — это колебания, происходящие в отсутствии внешних воздействий на систему, со строго определенной частотой, называемой частотой собственных колебаний системы. Эта частота зависит только от параметров системы. Примерами таких колебаний могут служить колебания математического и пружинного маятников.

Любые собственные колебания в реальной системе рано или поздно затухают. Чтобы колебания не затухали, необходимо воздействие внешней силы. Однако не всякая внешняя сила заставляет систему двигаться периодически. Например, невозможно раскачать качели, если действовать на них с постоянной по модулю и направлению силой. Внешняя сила тоже должна быть периодической.

Колебания тел под действием внешней периодической силы (в частном
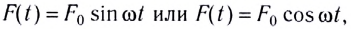
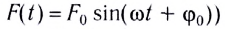
случае гармонической силы в общем случае называют вынужденными, а сила называется вынуждающей. Эксперименты показывают, что частота установившихся вынужденных колебаний всегда равна частоте вынуждающей силы.
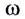
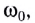
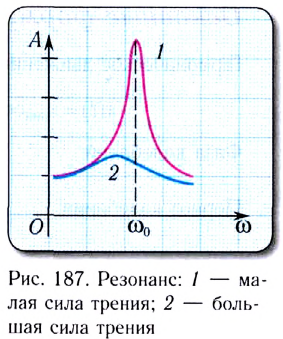
Амплитуда колебаний и энергия, передаваемая системе за период вынужденных колебаний, зависят от того, насколько различаются частота вынуждающей силы и частота собственных колебаний а также от величины трения в системе.

При вынужденных колебаниях возможно явление, называемое резонансом (от латинского слова resono — откликаюсь, звучу в ответ).

Резонанс — это явление резкого возрастания амплитуды вынужденных колебаний при действии на колебательную систему внешней силы с частотой, совпадающей с собственной частотой системы 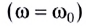(рис. 187).

При резонансе создаются оптимальные условия для передачи энергии внешнего источника системе, так как в течение всего периода работа внешней силы источника над системой положительна. Вспомните процесс раскачивания на качелях: если качели толкать с очень большой частотой или с очень малой, их практически невозможно будет раскачать. Если же подбирать частоту толчков, близкую к частоте собственных колебаний качелей, то раскачивание будет эффективным.

Основные формулы:

Гармоническое движение:

Фаза колебаний:

Период колебания:

Циклическая частота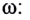

Уравнение гармонических колебаний:

Период колебаний пружинного маятника:

Период колебаний математического маятника:

Единицы измерения основных величин колебаний

Колебательное движение и свободные колебания

Колеблются деревья под действием ветра, поршни двигателя автомобиля под действием продуктов сгорания топлива. Мы можем разговаривать благодаря колебаниям голосовых связок гортани и слышать вследствие колебаний барабанных перепонок. Колебательным является биение сердца. C колебаниями связан и свет, который возникает при колебаниях молекул и атомов. C помощью электромагнитных колебаний, которые распространяются в пространстве, можно осуществлять радиосвязь, радиолокацию, лечить и диагностировать многие болезни.

В приведенных примерах колебаний на первый взгляд мало общего. Но при детальном исследовании приведенных примеров можно найти их общие свойства: различные по происхождению и природе колебания описываются одинаковыми уравнениями, имеют общие характеристики, это существенно облегчает их изучение и исследование.

Колебания, в которых состояние системы повторяется через одинаковые интервалы времени, называются периодическими.

Непериодические колебания не имеют постоянного периода колебаний и являются процессами, в которых состояние системы повторяется через произвольные и, как правило, неодинаковые интервалы времени. Такими, например, являются колебания веток дерева под действием порывов ветра.

Непериодические колебания не имеют постоянного периода колебаний.

Простейшими колебаниями являются так называемые гармонические колебания. Это колебания, в которых основные физические величины, касающиеся колебаний, изменяются по закону синуса или косинуса. Без изучения этих колебаний нельзя изучить более сложные колебания.

Колебания, в которых основные физические величины, касающиеся колебаний, изменяются по закону синуса или косинуса, называются гармоническими.

При изучении колебательных процессов для упрощения измерений и расчетов пользуются замкнутой системой, в которой тела взаимодействуют только в пределах определенной системы. Колебания, происходящие в замкнутой системе, называются свободными.

Примером свободных колебаний являются колебания пружинного маятника.

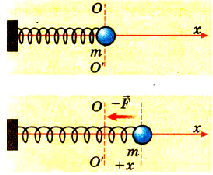
Рис. 3.1. Колебания пружинного маятника

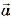
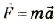
Если освободить грузик, то он начнет двигаться до.положения равновесия с ускорением . Согласно второму закону Ньютона .

В момент прохождения грузика через положение равновесия его скорость и кинетическая энергия будут максимальными (рис. 3.2).

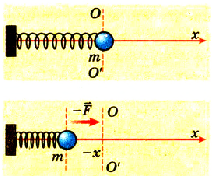
Рис. 3.2. Грузик движется влево

Имея определенную кинетическую энергию, грузик по инерции продолжает двигаться дальше (влево), выполняя работу по деформации пружины. Сила упругости, возникающая при этом, направлена к положению равновесия. Когда грузик окажется в крайнем левом положении, на него будет действовать сила упругости, направленная к положению равновесия (вправо). Под действием этой силы грузик начнет ускоренно двигаться до положения равновесия (вправо). Если предположить, что силы трения и сопротивления воздуха ничтожны, то процесс должен продолжаться бесконечно.

Записав совместно формулу второго закона Ньютона и закона Гука, получим уравнение движения грузика:

Отсюда,

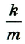
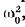
В этом уравнении величина всегда положительная, поскольку жесткость пружины и масса грузика не могут быть отрицательными. Поэтому эту величину обозначают символом , a уравнение движения тела па пружине записывают в виде

Общее уравнение колебаний:

Решением этого уравнения является периодическая функция

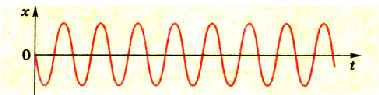
Puc. 3.3. График незатухающих гармонических колебаний

Воспользовавшись тем, что 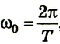получим формулу периода колебаний пружинного маятника:

Кроме смещения по гармоническим законам, изменяются скорость и ускорение движения груза.

Поскольку в реальных условиях в каждой системе действуют силы трения и сопротивления, то амплитуда колебаний будет постепенно уменьшаться (рис. 3.4).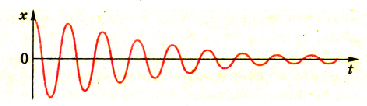

Puc. 3.4. График свободных колебаний

Свободные колебания в реальных условиях всегда затухающие, поскольку в каждой колебательной системе, действуют силы трения. Поэтому каждая следующая амплитуда колебаний будет меньше предыдущей. Если бы удалось создать идеальную систему, в которой не действуют силы трения, то колебания в этой системе были бы незатухающими. Поскольку такие идеализации применяются в физике для исследования колебаний, то частоту незатухающих колебаний в идеальной системе назвали собственной частотой.

Частоту колебаний в идеальной системе, в которой отсутствуют силы трения, называют собственной частотой.

Пример №3

Определить период колебаний грузика, который имеет массу 100 г и подвешен к пружине, коэффициент упругости которой 10 Н/м.

Ответ: период колебаний пружинного маятника равен 0,628 с.

Колебательное движение и вынужденные колебания

Во многих технологических процессах происходят колебания, которые должны быть долговременными.

Поэтому создают условия для получения незатухающих колебаний. C этой целью в технических установках применяют вынужденные колебания. Это колебания, происходящие под действием внешней силы, которая периодически изменяется. Такими, например, являются колебания поршней в автомобильном двигателе, происходящие вследствие периодического действия газа во время рабочего хода поршня.

Вынужденными колебаниями является и переменный ток. который возникает в рамке, вращающейся в магнитном поле.

Частота вынужденных колебаний определяется частотой действия вынуждающей силы.
Регулируя подачу горючего в цилиндр, можно изменять частоту колебаний поршней. Частота переменного тока определяется скоростью вращения ротора турбины.

Особый интерес представляет случай, когда периодическая внешняя сила, действует па тело, которое может совершать свободные колебания.

Если в начальный момент тело было неподвижным, то после начала действия периодической силы оно начинает колебаться со все возрастающей амплитудой. Через некоторое время амплитуда устанавливается постоянной и в дальнейшем не возрастает.

Это происходит потому, что вся энергия, приходящая в колебательную систему, идет на выполнение работы по преодолению сил трения в системе. Если изменять частоту вынуждающей силы, то можно обнаружить явление резонанса. При частоте, равной собственной частоте колебаний системы, резко возрастает амплитуда. Сильно раскачать качели можно только в том случае, если подталкивать их будем «в такт» с частотой собственных колебаний качели. Явление резкого возрастания амплитуды вынужденных колебании называют резонансом.

Резонанс наступает тогда, когда частота действия вынуждающей силы будет равна собственной частоте колебаний системы.
f_вын=f_соб

После повышения частоты выше резонансной амплитуда начнет убывать. Для каждой колебательной системы существует определенная частота, при которой наступает резонанс.

На рисунке 3.7 показана графическая зависимость амплитуды колебаний от частоты вынуждающей силы. Высота резонансной кривой, изображенной на этом рисунке, зависит от значения сил трения в колебательных системах. Так. график показывает, что резонансные частоты в трех колебательных системах одинаковые, но силы трения будут различными. Выше кривая меньше силы трения.

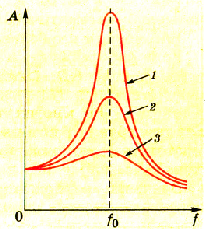
Рис. 3.7. Резонансные кривые для разных значений силы трения

C явлением резонанса мы встречаемся довольно часто и в быту, и в технике. Действие этого явления может быть как полезным, так и вредным. Так, чтобы выехать из лужи или песка, водитель с определенной частотой включает и выключает сцепление, раскачивая автомобиль. Увеличение амплитуды колебаний автомобиля содействует его выезду из выбоины.

Достоянием истории стала катастрофа с Бруклинским мостом в Нью-Йорке, который разрушился вследствие резонанса.

Колебательное движение и математический маятник

Одной из систем, которые могут совершать колебания, является нитяный маятник. Ото тело небольших размеров, подвешенное на длинной нерастяжёной нити. Выведенная из положения равновесия, эта система может совершать колебания.

Рассмотрим его более подробно.

Если система будет в равновесии, то на маятник будут действовать только сила тяжести и сила упругости нити. Их равнодействующая будет равна нулю (рис. 3.8). Естественно, что в таком случае шарик не будет двигаться.

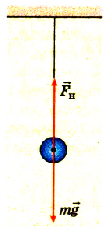
Рис. 3.8.Нитяный (математический) маятник в положении равновесия

Если груз вывести из положения равновесия, то равнодействующая F сил тяжести и упругости уже будет отличной от нуля (рис. 3.9).

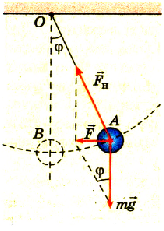
Pиc. 3.9. Равнодействующая сил тяжести и упругости направлена к положению равновесия

Значение равнодействующей определим по рисунку на основании анализа параллелограмма сил:

Применим к описанию движения математического маятника второй закон Ньютона с учетом, что смещение груза направлено в сторону» противоположную равнодействующей:

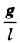
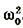
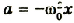
Величина всегда положительная. Поэтому ее можно обозначить . Тогда уравнение движения математического маятника будет иметь вид: .

Математический маятник совершает гармонические колебания по уравнению, решением которого является функция: х = Аsin(ωt + а).

Из курса математики известно, что решением этого уравнения является функция х =Asin(ωt + а). Поскольку эта функция гармоническая, то и колебания математического маятника называют гармоническими.

Таким образом, период колебаний математического маятника зависит от длины подвеса и ускорения свободного падения.

Период колебаний математического маятника зависит от длины подвеса и ускорения свободного падения:

Зависимость частоты колебаний математического маятника находят из соотношения

,

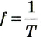
Пример №4

Маятник длиной 150 см за 300 с совершает 122 колебания. Чему равно ускорение свободного падения?

Согласно этой формуле

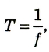
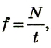
Если учесть, что а то получим

Подставив значения физических величин, получим

Ответ: ускорение свободного падения в этом случае составляет 9,78 .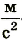

Энергия колебательного движения

В механике различают кинетическую и потенциальную энергии. Кинетическая энергия определяется массой тела и его скоростью.

Потенциальную энергию тела в поле земного тяготения определяют по формуле E_n = mgh, потенциальную энергию упруго деформированного тела (например, пружины) по формуле .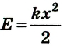

Если внимательно рассмотреть движение грузика на пружине (см. рис. 3.1 и 3.2), то здесь периодически будут изменяться как скорость тела, так и сила упругости пружины. Таким образом, периодически будут изменяться как кинетическая, так и потенциальная энергии. Кинетическая энергия будет максимальной в момент прохождения телом положения равновесия, когда его скорость будет максимальной. Потенциальная энергия приобретет максимальное значение через четверть периода, кода будет максимальным отклонение от положения равновесия.

До сих пор мы рассматривали случаи колебаний, пренебрегая потерями механической энергии. Для этого случая действует закон сохранения механической энергии:

Соответственно этому закону максимальное значение потенциальной энергии будет при максимальном отклонении, когда кинетическая энергия (и скорость) равна нулю:

Если потери механической энергии в системе отсутствуют, то

Из последнего уравнения можно рассчитать скорость, с которой тело проходит положение равновесия.

Колебательное движение и механические волны

Колебания как процесс могут распространяться в пространстве. Для подтверждения этого подвесим на нити, закрепленной в штативе, несколько маятников и один из них приведем в колебательное движение (рис. 3.11).

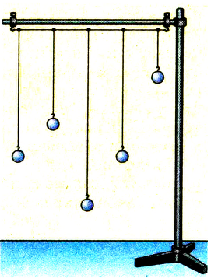
Рис. 3.11. Маятники на нити

Спустя некоторое время все маятники будут совершать колебания. Таким образом, механические колебания могут предаваться от одного тела к другому через упругие связи. Подобное происходит и в природе.

Как и любое другое физическое явление, волна имеет свои определенные характеристики.

Одной из величин, характеризующих волну, является скорость волны. Все известные науке волны распространяются не мгновенно, а на протяжении определенного времени, с определенной скоростью.
Каков же механизм образования волн?

Проанализировав рассмотренные ранее примеры, можно отметить, что механическая волна распространяется в упругой среде. Для того чтобы представить процесс распространения волны в упругой среде, промоделируем его с помощью шариков некоторой массы, соединенных между собой пружинками (рис. 3.12-а). Если сообщить определенный импульс левому крайнему шарику (рис. 3.12-б), то он начнет движение вверх, растягивая пружинку. Вследствие этого на второй шарик начнет действовать сила упругости растянутой пружинки, которая будет смещать шарик в том же направлении. Проявление инерции задержит движение второго шарика, который будет отставать от первого шарика (рис. 3.12-в).

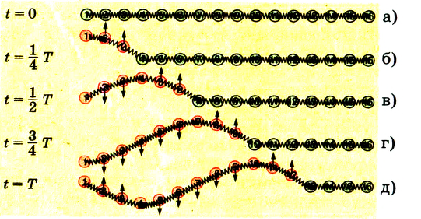
Pиc. 3.12. Модель процесса образования поперечной волны

Если первый шарик привести в колебательное движение, то второй также начнет колебаться, но с некоторым отставанием по фазе. Третий шарик под действием силы упругости второй пружинки также начнет колебаться, еще более отставая по фазе. В итоге все шарики будут колебаться с одинаковой частотой, но со сдвигом по фазе. При этом цепочкой побежит поперечная волна.

Если первому шарику придать импульс, направленный вдоль прямой, соединяющей оси шариков, то цепочкой распространится продольная волна. Ее можно наблюдать на длинной горизонтальной пружине, одним концом закрепленной на стене (рис. 3.13): после удара по торцу пружины образуются сгустки и разрежения витков, которые будут двигаться вдоль пружины как продольная волна.

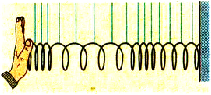
Pиc. 3.13. Распространение продольной волны

Если повторить модельный опыт образования волны в цепочке из пружинок и шариков (рис. 3.12), то можно заметить, что когда первый шарик проходит положение равновесия и движется вверх, то на определенном расстоянии от него существует шарик, который, проходя положение равновесия, также движется вверх, т. е. колебания совершаются в одной фазе.

Расстояние между двумя соседними точками волны, которые колеблются в одинаковой фазе, называют длиной волны (рис. 3.14). Например, это расстояние между двумя гребнями волны, образовавшейся от брошенного в воду камня. Длина волны обозначается буквой греческого алфавита λ (лямбда).

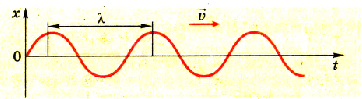
Puc. 3.14. Расстояние между двумя соседними точками волны. колеблющимися водной фазе

За один период она распространяется на расстояние, равное длине волны, Поэтому скорость распространения волны можно определить через эти величины:

Длина волны равна произведению скорости распространения на период: λ = υT.

Так как период связан с частотой формулой

Возможно иное определение длины волны: это расстояние, на которое распространяется волна за один период.

Длина волны является универсальной характеристикой для волновых процессов различной природы.

Пример №5

Лодка качается на волнах, распространяющихся со щ скоростью 2,5 м/с. Расстояние между гребнями волн 2,5 м. Найти период колебаний лодки.

Отсюда

Подставив значения физических величин, получим

Oтвет: период колебания лодки 3,2 с.

Колебательное движение и звуковые волны

Звук сопровождает человека на протяжении всей жизни. Он является основным средством общения между людьми, его используют в различных технологических процессах. Как вы знаете, источником звука является колеблющееся тело. Колеблются ножки камертона, излучая звук определенного тона, диффузор громкоговорителя, воссоздавая голос человека или звучание музыкального инструмента. Распространение этих колебаний и воспринимается нами как звук.

Звук является продольной волной, которая распространяется только в упругой среде, в частности в воздухе, воде, металлах, дереве, пластмассе и т. п.

Роль воздуха в распространении звука впервые была раскрыта в 1660 г. английским физиком Р. Бойлем, который открыл, что под колпаком вакуумного насоса, если из-под него выкачан воздух, звук не распространяется.

Звук начали исследовать очень давно. Поэтому для его характеристики применяют специфические величины. Так, высота тона, о которой говорят музыканты, обозначает частоту колебаний: чем больше частота, тем выше тон. Громкость звука связана с амплитудой колебаний: чем больше амплитуда, тем громче звук.

Звуковые волны имеют свойство отражаться от препятствий. Если звуковая волна падает на сплошное препятствие (стену, гору), то она отражается, и мы слышим эхо. Свойство отражаться используют инженеры создавая приборы для определения глубины воды под днищем корабля. Его назвали эхолотом, или эхолокатором (рис. 3.15).

Puc. 3.15. Схема объясняющая принцип действия эхолокатора

Излучатель посылает узкий импульсный пучок звуковых волн в сторону дна, я специальный микрофон улавливает отраженный сигнал. Измеряя интервал времени между посылкой и приемом сигнала, специальная аппаратура определяет расстояние до дна.

Инфразвуки н целом отрицательно действуют на живой организм. Поэтому необходимо устранять их источники или применять профилактические меры безопасности. Так, на производствах, где производственные технологии связаны с применением мощных низкочастотных колебаний, используют различные средства изоляции рабочих от их воздействия. Например, известны случаи, когда установка нового мощного вентилятора не повысила производительности труда рабочих, а наоборот, повысила их утомляемость.

Колебательный контур и возникновение электромагнитных колебаний в колебательном контуре

Кроме механических колебаний, н природе существуют электромагнитные колебания. Они возникают в системе, которая называется колебательным контуром. Это электрическая цепь, состоящая из катушки индуктивности и конденсатора, соединенных между собой параллельно (рис. 3.16).

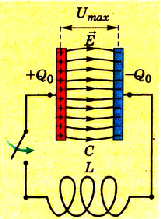
Pиc. 3.16. Cxerna колебательного контура

Обычно сопротивление проводников в такой цепи незначительно. Для получения колебаний в колебательном контуре сначала заряжают конденсатор, сообщая ему заряд Q₀. Тогда в начальный момент времени между обкладками конденсатора возникает электрическое поле. Полная энергия контура в это время равна энергии заряженного конденсатора:

При замыкании ключа конденсатор начинает разряжаться и в контуре возникает возрастающий по значению ток. Вследствие разряда конденсатора энергия электрического поля уменьшается; она превращается в энергию магнитного поля катушки, по которой проходит ток I:

В идеальном колебательном контуре полная энергия сохраняется и остается равной энергии электрического поля конденсатора после его зарядки. В любой произвольный момент времени она равна сумме энергий электрического поля конденсатора и магнитного поля катушки:

В момент времени, когда конденсатор полностью разрядится, энергия электрического поля становится равной нулю, а энергия магнитного поля достигает максимального значения:

После этого сила тока в контуре начинает уменьшаться, Уменьшается и магнитный поток. По закону электромагнитной индукции, изменению тока противодействует ЭДC самоиндукции, которая возникает при изменении магнитного потока. Поэтому конденсатор начинает перезаряжаться, и между его обкладками Снова возникает электрическое поле.

Когда перезарядка прекратится, на обкладках конденсатора будет заряд, равен первоначальному, по с противоположным знаком.

В дальнейшем процесс повторяется, но в обратном направлении. Через определенное время система возвращается в первоначальное положение, и начинается самопроизвольный цикл периодической зарядки и перезарядки конденсатора че- рез катушку. При отсутствии потерь па нагревание проводников и излучение колебания в колебательном контуре будут незатухающими.

В реальных условиях колебания в колебательном контуре будут затухающими. Поэтому их нужно считать свободными. Их период и частота зависят от параметров колебательного контура емкости конденсатора и индуктивности катушки. Выдающийся английский физик В. Томсон установил, что

Если колебательный контур включить в электрическую цепь переменного тока, то в нем возникнут вынужденные колебания, частота которых будет равна частоте переменного тока. Их амплитуда будет зависеть от сопротивления проводников контура и от соотношения между частотой переменного тока и собственной частотой контура. В случае совпадения этих частот в контуре будут возникать колебания, амплитуда которых резко возрастает. Таким образом, в колебательном контуре будет появляться резонанс. Это явление используют в радиоприемниках, когда с помощью настройки контура на определенную частоту’ принимают сигналы определенной станции. Изменяя индуктивность катушки или емкость конденсатора, мы изменяем собственную частоту контура. Если собственная частота контура совпадает с частотой определенного сигнала, в контуре, благодаря резонансу, возникает значительный ток, который передается в специальное устройство для дальнейшего усиления и обработки.

Образование электромагнитных волн

Электромагнитные колебания распространяются в пространстве в виде электромагнитных волн. В них происходят взаимные превращения электрического и магнитного полей, которые вместе образуют электромагнитное поле, распространяющееся в пространстве.

Процесс распространения электромагнитных колебаний называется электромагнитной волной.

Для образования электромагнитных волн, как и волн любой природы, необходимо иметь систему, в которой возникают электромагнитные колебания. Для электромагнитных колебаний такой системой будет колебательный контур, состоящий из конденсатора и катушки индуктивности.

Современные электронные системы позволяют поддерживать в нем незатухающие колебания на протяжении длительного времени, что в свою очередь создает условия для длительного излучения электромагнитных волн. По этому принципу работают вещательные радиостанции, телевидение и другие средства связи.

Однако сам по себе колебательный контур не может излучать электромагнитные волны, поскольку электрическое поле сосредоточено между обкладками конденсатора и вне контура не проявляется.

Переменные магнитные поля сосредоточены в основном внутри катушки и не распространяются за пределы контура. Исследования показали, что электромагнитные волны могут излучаться в пространство только открытым колебательным контуром, который в простейшем виде состоит из двух линейных проводников, связанных друг с другом катушкой индуктивности (рис. 3.17).

Рис. 3.17. Открытый колебательный контур

Для возбуждения электромагнитных колебаний в открытом контуре существуют различные способы. Наиболее распространенный из них способ, когда катушка индуктивности открытого контура образует индуктивную связь с контуром генератора незатухающих колебаний (рис. 3.18).

Рис. 3.17. Связь открытого контура с контуром генератора

Благодаря электромагнитной индукции в катушке открытого колебательного контура L_e появляется переменная ЭДС, возбуждающая в проводниках переменный ток. Поскольку электроны, образующие переменный ток в проводниках, движутся ускоренно, то проводники открытого колебательного контура имеют переменное электромагнитное ноле.

Открытый колебательный контур, в котором происходят электромагнитные колебания, имеет переменные магнитное и электрическое поля. Так, переменное электрическое поле открытого колебательного контура индуцирует «собственное» переменное магнитное поле.

Переменное электрическое поле открытого колебательного контура будет индуцировать «собственное» переменное магнитное поле.

Индуцированное переменное мигни гное поле, в свою очередь, будет возбуждать индуцированное электрическое поле.

Графически электромагнитную волну можно изобразить в виде двух синусоид, расположенных во взаимно перпендикулярных плоскостях (рис. 3.19).

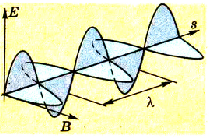
Puc. 3.19. Графическое изображение электромагнитные волны

Этот рисунок показывает существующую зависимость значений векторов напряженности электрического поля E и магнитной индукции В от расстояния в направлении распространения волны. По направлению эти векторы органически связаны между собой и с вектором скорости распространения волны 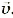. Их колебания происходят во взаимно перпендикулярных плоскостях, причем вектор скорости всегда перпендикулярен к плоскости колебаний векторов E и В, а его направление определяется по правилу правого винта.

Если правый винт вращать в направлении от вектора E к вектору В кратчайшим путем, то его поступательное движение покажет направление вектора скорости

Аналитически колебательный процесс, которым является электромагнитная волна, представляется двумя уравнениями для модулей векторов Е и В:

Таким образом, распространение электромагнитных волн происходит как возбуждение связанных между собой электрического и магнитного переменных полей в направлении, определяемом по правилу правого винта.

Шкала электромагнитных излучений

Во время исследований, длительное время проводившихся учеными, не обнаружили каких-либо ограничений относительно частоты или длины электромагнитного излучения. Т. е. нет смысла вести речь о самой короткой или самой длинной волне, ограничивая диапазон электромагнитных волн. Речь может быть лишь об определенном диапазоне воли, открытых и исследованных современной наукой.

Для наглядного представления о разнообразии электромагнитных излучений и зависимости их свойств от длины волны составлена шкала, один из вариантов которой представлен на форзаце. Они расположены по определенным условным диапазонам, не имеющим четких границ: низкочастотные волны, радиоволны, инфракрасное излучение, видимый свет, ультрафиолетовое, рентгеновское и гамма-излучение. Такое деление произведено с учетом природы их возникновения и особенностей взаимодействия с веществом. Например, если радиоволны образуются электромагнитными колебаниями, возбуждаемыми в колебательном контуре определенной емкости и индуктивности, чем и определяется длина волны, то гамма-излучение возникает как следствие ядерных процессов, связанных с радиоактивным распадом.

Существуют также отличия и во взаимодействии электромагнитных волн с веществом и в особенностях распространения в пространстве. Если видимый свет полностью поглощается топким слоем бумаги, то рентгеновское и гамма-излучения могут проникать не только через человеческое тело, но и через металлы.

Рассмотрим шкалу электромагнитного излучения подробнее.

Низкочастотное излучение возникает в результате работы различных электротехнических устройств и приборов, в которых используется переменный ток низкой частоты. Оно имеет низкую энергию и до сих пор не нашло практического применения ни в информационных, ни в энергетических технологиях.

Радиоволны разделены на диапазоны длинных, средних, коротких и ультракоротких волн. Поводом для такого деления послужили особенности их распространения.

В широком диапазоне радиоволны делятся на длинные, средние, короткие и ультракороткие.

Инфракрасное излучение называют также тепловым, так как оно наблюдается у всех нагретых тел.

В широком понимании оптический диапазон охватывает инфракрасное излучение, видимый свет и ультрафиолетовое излучение. Инфракрасное излучение лежит за пределами восприятия глазом волн, длина которых больше 760 нм и простилается к 0,1 мм. Их излучают все нагретые тела, благодаря чему мы ощущаем теплоту. При повышении температуры длина волны, на которую приходится максимум излучения, смещается в область более коротких волн. Инфракрасное излучение слабо поглощается воздухом и хорошо отражается от поверхности твердых тел. Это их свойство применяют в приборах «ночного видения».

Со стороны коротковолновой части диапазона видимых волн находится диапазон ультрафиолетового излучения, которое не воспринимается человеческим глазом. Вместе с тем, взаимодействуя с веществом, это излучение может вызывать излучение видимого света. Нм этом основан метод неразрушающего анализа вещества, когда по цвету излучения определяют наличие тех или иных веществ в смеси. Широко известен способ применения ультрафиолетового излучения для выявления фальшивых денежных купюр.

Ультрафиолетовое излучение практически полностью поглощается обычным оконным стеклом.

Ультрафиолетовое излучение имеет сильное бактерицидное действие, его широко применяют для стерилизации, медицинских инструментов, различных медицинских материалов. Невозможно представить больничную палату без ламп, излучающих ультрафиолетовый свет.

Вместе с тем ультрафиолетовое излучение может отрицательно воздействовать на человеческий организм, попадая на кожу или слизистую оболочку. Оно вызывает ожоги, которые плохо поддаются лечению.

Рентгеновское излучение известно многим из нас как средство медицинского исследования организма. Впервые его получил и исследовал известный физик, украинец по происхождению И. Пулюй (1845-1918). Но случилось так, что первым сообщил об открытии немецкий физик В. Рентген (1845-1928). За это открытие ему позднее была присуждена Нобелевская премия в области физики.

Рентгеновское излучение имеет высокую проницательную способность, оно может проникать сквозь толстые слои вещества и даже металлов. Его используют в промышленности для выявления внутренних дефектов металлических изделий, в медицине для исследования внутренних органон человека, в научных исследованиях строения вещества.

Следующий диапазон — гамма-излучение — относится к ядерным процессам и связан с процессами, происходящими в атомных ядрах.

Радиоволны

Радиоволны принадлежат к диапазону электромагнитных ноли длиной от нескольких километров до нескольких десятков километров. В высокочастотной области диапазона радиоволны плавно переходят в инфракрасное излучение, хотя четкая граница не установлена. В своей низкочастотной части диапазона радиоволны граничат с низкочастотным излучением, которое образуется при работе электротехнических устройств, использующих переменный ток низкой частоты.

Справочный материал по колебательному движению

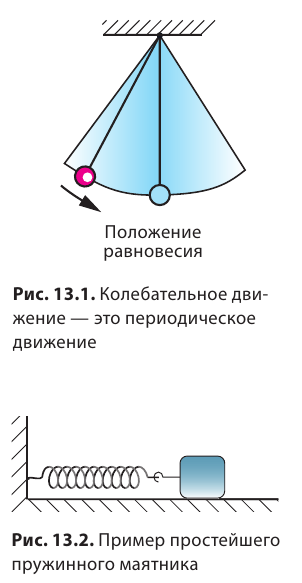
Еще в древности люди, наблюдая за Солнцем и Луной, определили единицы времени: год, месяц, сутки и др. Были созданы солнечные часы, затем водяные, огневые, песочные. Однако настоящая революция в конструкции часов произошла после выяснения свойств колебательного движения.

Подвесим груз на нить, отклоним его от положения равновесия и отпустим. Груз начнет колебаться, то есть двигаться от одного крайнего положения к другому, повторяя это движение через некоторый интервал времени. Таким образом, колебательное движение имеет важную общую черту с равномерным движением по окружности: оба движения являются периодическими (рис. 13.1).

Изучаем маятники:

Груз, колеблющийся на нити или на пружине, — пример простейшего маятника.

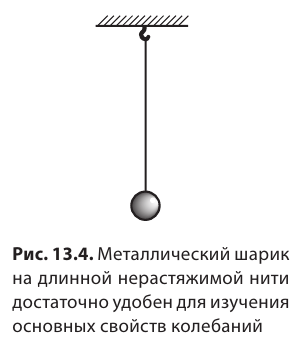
Маятник — это твердое тело, которое совершает колебания вследствие притяжения к Земле или в результате действия пружины. Маятники используют во многих физических приборах. Особенно важным является использование маятников в часах: периодичность колебаний дает возможность осуществлять отсчет времени. Маятники, колеблющиеся благодаря действию пружины, называют пружинными маятниками (рис. 13.2). Колебания пружинного маятника зависят от свойств пружины и мас­сы тела. Маятники, колеблющиеся благодаря притяжению к Земле, называют физическими маятниками (рис. 13.3). Их колебания достаточно сложны, поскольку зависят от массы, геометрических размеров, формы маятника и т. д. Чтобы размеры и форма тела не влияли на его колебания, нужно взять нить, длина которой достаточно велика по сравнению с размерами тела, — в таком случае тело можно считать материальной точкой. При этом нить должна быть легкой и довольно тонкой, а чтобы во время колебаний тело было на неизменном расстоянии от точки подвеса, — нерастяжимой. Небольшой металлический шарик диаметром 1–2 см, подвешенный на тонкой нерастяжимой нити длиной 1–2 м, вполне может служить маятником, на колебания которого не будут влиять размеры, масса тела и свойства нити (рис. 13.4)*. Такой маятник называют нитяным.

Что такое амплитуда колебаний

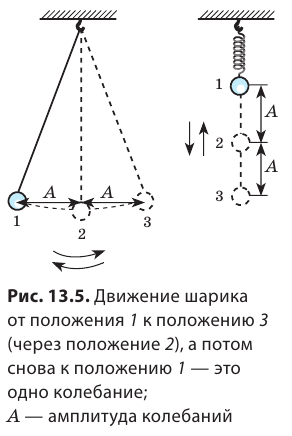
Наблюдая за колебаниями маятника, нетрудно заметить, что есть определенное максимальное расстояние, на которое колеблющееся тело удаляется от положения равновесия. Это расстояние называют амплитудой колебаний (рис. 13.5).

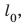
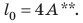
Амплитуда колебаний — это физическая величина, равная максимальному расстоянию, на которое отклоняется тело от положения равновесия во время колебаний. Амплитуду колебаний обозначают символом A. Единица амплитуды колебаний в СИ — метр: [A]= м. За одно колебание тело проходит путь который примерно равен четырем амплитудам: 4 Определяем период и частоту колебаний

Колебательное движение является периодическим движением, поэтому оно характеризуется такими физическими величинами, как период колебаний и частота колебаний.

В данном случае длина нити считается также длиной маятника.

В случае с нитяным маятником данное равенство является приблизительным, так как тело движется по дуге окружности, длина которой больше расстояния, называемого амплитудой колебаний. Но если амплитуда колебаний мала (намного меньше длины маятника), этим различием обычно пренебрегают.

Период колебаний — это физическая величина, равная времени, за которое происходит одно колебание. Период колебаний, как и период равномерного движения по окружности, обозначают символом T и вычисляют по формуле: 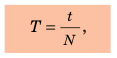, где t — время наблюдения; N — количество колебаний за это время. Единица периода колебаний в СИ — секунда: [T]= с.

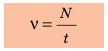
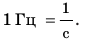
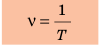
Частота колебаний — это физическая величина, которая равна количеству колебаний за единицу времени. Частоту колебаний обозначают символом ν («ню») и вычисляют по формуле: Единица частоты колебаний в СИ — герц ( Г ц ) ; названа так в честь Генриха Герца (рис. 13.6). Если тело за одну секунду осуществляет одно колебание, то частота его колебаний равна одному герцу: Частота ν и период T колебаний — взаимно обратные величины: У маятников есть очень важное свойство: если амплитуда колебаний маятника намного меньше его длины, то частота и период колебаний маятника не зависят от амплитуды колебаний. Это свойство малых колебаний открыл Галилео Галилей*, и именно оно лежит в основе работы механических часов.

Различия затухающих от незатухающих колебаний

Выведем качели из состояния равновесия и отпустим. Качели начнут колебаться. Такие колебания называют свободными. Если на качели не влиять, то через некоторое время амплитуда их колебаний заметно уменьшится, а со временем колебания прекратятся вовсе. Колебания, амплитуда которых со временем уменьшается, называют затухающими колебаниями.

Свободные колебания всегда являются затухающими. Затухают с течением времени свободные колебания языка колокола, струны гитары, ветки дерева. Что следует сделать, чтобы амплитуда колебаний качелей со временем не уменьшалась, то есть чтобы их колебания были незатухающими? Незатухающие колебания — это колебания, амплитуда которых не изменяется со временем. Незатухающие колебания осуществляет, например, игла швейной машины, пока работает ее механизм (рис. 13.7).

Пример №6

Небольшой тяжелый шарик, подвешенный на нерастяжимой нити длиной 1 м, отклонили от положения равновесия и отпустили. За 30 с шарик совершил 15 колебаний. Какое расстояние пройдет шарик за 36 с, если амплитуда его колебаний — 5 см? Колебания считайте незатухающими. Анализ физической проблемы. Амплитуда колебаний намного меньше длины нити, поэтому можно считать, что за одно колебание шарик проходит путь, равный четырем амплитудам (4A). Если определить количество колебаний за 36 с, то можно найти расстояние, которое прошел шарик. Количество колебаний найдем, определив время одного колебания, то есть период колебаний.

,,,.

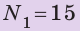
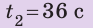
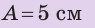
Решение:

Найдем период колебаний:

Найдем количество колебаний за 36 с:

Определим расстояние, которое проходит шарик за одно колебание:

Определим путь, который пройдет шарик за 36 с:

Анализ результатов. За одно колебание шарик проходит 20 см; время колебаний больше периода колебаний, поэтому пройденное шариком расстояние будет больше 20 см. Следовательно, результат правдоподобен.

Ответ:

Итоги:

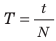
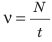
Колебательное движение (колебания) — периодическое движение. Различают затухающие и незатухающие колебания. Амплитуда А колебаний — это физическая величина, равная максимальному расстоянию, на которое тело отклоняется от положения равновесия во время колебаний. Период Т колебаний — это физическая величина, равная времени, за которое происходит одно колебание: . Единица периода колебаний в СИ — секунда (с). Частота ν колебаний — это физическая величина, равная количеству колебаний за единицу времени: . Единица частоты колебаний в СИ — герц (Гц). Частота и период колебаний — взаимно обратные величины:

«Механическое движение»:

Вы изучали механическое движение и его характеристики, узнали о видах механического движения: прямолинейное движение, движение по окружности, колебательное движение.

Вы ознакомились с некоторыми основными понятиями механики.

Вы научились различать виды механического движения.

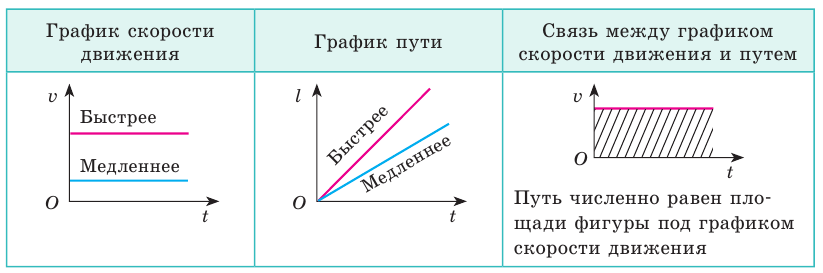
Вы научились исследовать равномерное движение с помощью графиков пути и графиков скорости движения.

Вы исследовали некоторые механические движения.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник