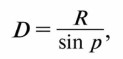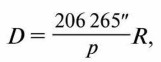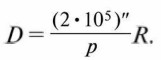чем дальше расположен объект тем
Определение расстояний в Солнечной системе. Горизонтальный параллакс
Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является её радиус.
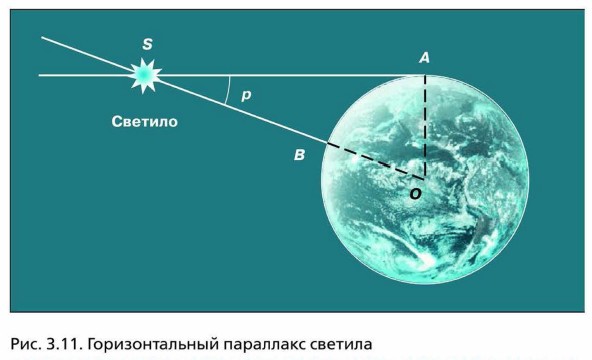
Горизонтальным параллаксом (р) называется угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения (рис. 3.11).
Из треугольника OAS можно выразить величину — расстояние OS = D:
где R — радиус Земли. По этой формуле можно вычислить расстояние в радиусах Земли, а зная его величину, — выразить расстояние в километрах.
Очевидно, что чем дальше расположен объект, тем меньше его параллакс. Наибольшее значение имеет параллакс Луны, который меняется в связи с тем, что Луна обращается по эллиптической орбите, и в среднем составляет 57′. Параллаксы планет и Солнца значительно меньше. Так, параллакс Солнца равен 8,8″. Такому значению параллакса соответствует расстояние до Солнца, примерно равное 150 млн км. Это расстояние принимается за одну астрономическую единицу (1 а. е.) и используется при измерении расстояний между телами Солнечной системы.
Известно, что для малых углов sin р ≈ р, если угол р выражен в радианах. В одном радиане содержится 206 265″. Тогда, заменяя sin р на р и выражая этот угол в радианной мере, получаем формулу в виде, удобном для вычислений:
или (с достаточной точностью)
Во второй половине XX в. развитие радиотехники позволило определять расстояния до тел Солнечной системы посредством радиолокации. Первым объектом среди них стала Луна. Затем радиолокационными методами были уточнены расстояния до Венеры, Меркурия, Марса и Юпитера. На основе радиолокации Венеры величина астрономической единицы определена с точностью порядка километра. Столь высокая точность определения расстояний — необходимое условие для расчётов траекторий полёта космических аппаратов, изучающих планеты и другие тела Солнечной системы. В настоящее время благодаря использованию лазеров стало возможным провести оптическую локацию Луны. При этом расстояния до лунной поверхности измеряются с точностью до сантиметров.
Параллакс: глубинное зрение
Как мы определяем глубину — расстояние от нашего местоположения до другого объекта? Для этого существует несколько способов, и один из самых распространённых и простых для понимания включает в себя такое геометрическое явление, как параллакс. Этот чрезвычайно простой принцип используется нашими глазами и мозгом для формирования нашего трёхмерного изображения мира, а астрономы столетиями используют его для определения расстояний (или относительных расстояний) от Земли до астрономических объектов.
Ещё один распространённый способ определять расстояния включает в себя отправку волны (звука, света, чего-то ещё), распространяющейся с известной скоростью, которая отражается от объекта и возвращается к нам; время, затраченное на возврат волны — эхо — сообщает нам расстояние до объекта. По этому принципу летучие мыши определяют расстояние до пищи и препятствий, а также работает радар.

Рис. 1
Мы воспринимаем параллакс, даже не думая о нём, каждый раз, когда двигаем головой. Представьте, что произойдёт, Если ваш друг спрячется от вас, встав в нескольких метрах за крупным деревом (рис. 1, в центре). Если вы достаточно далеко отодвинетесь влево или вправо, вашего друга станет видно (рис. 1, слева и справа). Мы знаем, что всё дело просто в перспективе; при определённом угле зрения дерево уже не будет загораживать вам вашего таинственного друга. Геометрически происходящее изображено на рис. 1. Когда вы двигаетесь влево и вправо, смотря вперёд, близлежащие объекты меняют свой угол по отношению к тому, что находится прямо перед вами, быстрее, чем объекты, расположенные дальше. Из скорости изменения угла при вашем движении — из параллакса движения — вы можете понять, насколько далеко расположен объект.
Каждый ребёнок это знает, поскольку, когда вы выглядываете из окна движущейся машины, фонарные столбы проносятся мимо очень быстро, удалённые здания проходят медленнее, а Луна, находящаяся настолько далеко, что угол зрения по отношению к наблюдателю не меняется на ощутимую величину, пока машина едет по шоссе, как будто бы двигается вместе с машиной. Именно небольшой параллакс, являющийся следствием огромного расстояния, заставляет луну «следовать за машиной».
Все, кто смотрел старые двумерные мультфильмы (и многие современные), такие, как Флинстоуны, знают, что этот факт используется, чтобы изобразить глубину. Когда персонажи путешествуют в автомобиле, двигаясь слева направо, автомобиль рисуют неподвижным, деревья рисуют в другом слое, который с высокой скоростью передвигается справа налево, а холмы в удалении рисуют на третьем слое, который двигается справа налево чуть медленнее (см. рис. 2).

Рис. 2
Наша способность воспринимать глубину, даже не двигая головой, основана на том же принципе. Левый и правый глаз видят мир с немного разных углов. Попробуйте разместить пару объектов — неважно, каких, пусть даже это будут большие пальцы рук — так, чтобы один из них был в два раза дальше другого, и находился прямо за ним. Закройте левый глаз и посмотрите на них правым; затем поменяйте глаза; потом снова поменяйте, и сделайте так несколько раз — и вы увидите, что объекты двигаются, как на рис. 1, только ваш левый глаз увидит ближайший объект справа от того, что дальше, а правый глаз увидит его чуть левее.
Так почему вы воспринимаете эти объекты при помощи обоих глаз так, будто они находятся один за другим? У вашей оптической системы есть очень хитрый обработчик информации — своего рода компьютер. Для вас он создаёт не такую картину мира, какую непосредственно видят ваши глаза, а выстроенную на её основе при помощи сложных преобразований картину. Воспринимать глубину вам позволяет информация, полученная от двух глаз и скомбинированная вместе (это в основном — хотя параллакс движения тоже вносит свою лепту). Ни один из ваших глаз не может определить глубину, если вы стоите неподвижно. Попробуйте закрыть глаза, повернуться в другую сторону и открыть один глаз. Можете ли вы точно описать расстояние до предметов? Мир выглядит более плоским, более двумерным, чем обычно. С обоими открытыми глазами у вас нет таких проблем. Это использование двух изображений для использования трёхмерной карты мира называется стереоэффектом.
Но даже с одним открытым глазом вы можете довольно быстро оценить глубину, если подвигаете головой. Ваш мозг способен использовать параллакс движения — более быстрое изменение угла зрения на близлежащие объекты по отношению к отдалённым при движении влево или вправо — чтобы помочь восстановить часть информации о глубине, которая обычно получается сравнением вида из двух разных глаз (рис. 2).

Рис. 3
Какие основные подсчёты использует наша оптическая система? Простейший случай показан на рис. 3. Допустим, объект находится прямо перед вами. Если ваши глаза находятся на расстоянии R друг от друга, а ваш левый глаз видит объект под углом α правее по отношению ко взгляду прямо вперёд, а правый глаз видит объект под углом α левее, тогда согласно простейшей геометрии прямоугольных треугольников, расстояние D до объекта будет равняться
Из формулы видно, что когда D меньше, угол, на который линия взгляда на объект отстоит от прямого взгляда, становится больше. Именно этого мы и ожидаем от параллакса.
В более общем случае, показанном на рис. 4, когда объект находится не прямо перед вами, получается чуть более сложным, как и тригонометрические формулы, но в нём работает тот же самый основной принцип и в итоге его не так уж сложно подсчитать. Ваш мозг проделывает такие подсчёты так быстро (используя технику, которую мы пока ещё не раскрыли), что вы об этом и не подозреваете.
Для достаточно удалённых объектов угол α оказывается слишком малым для того, чтобы его восприняли ваши глаза и мозг. В этот момент ваше чувство глубины пропадает. Поэтому Луна не кажется расположенной ближе, чем звёзды; они находятся слишком далеко, чтобы ощутить глубину. Также вашего ощущения глубины обычно не хватает, чтобы понять, пройдёт ли самолёт перед или за горой вдалеке. Но это просто ограничение ваших глаз.

Рис. 4
Как определить расстояние до более удалённых объектов? Есть два варианта; разработать научный инструмент, способный измерять углы точнее, чем ваш глаз; увеличить R, чтобы сравнивать не вид из глаз, а, например, вид из двух камер, стоящих в нескольких метрах друг от друга, или даже в разных местах континента. А когда астрономы хотят измерить самые большие расстояния, какие только можно измерить при помощи параллакса, они сравнивают изображения удалённой звезды, сделанные с разницей в шесть месяцев, чтобы получить максимальное расстояние R на основании того, что Земля в течение года проходит довольно большое расстояние. Детали этих техник отличаются, но основной принцип тот же, что показа на рис. 3 и рис. 4 — принцип параллакса.
ТЕСТ ПО АСТРОНОМИИ: ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ В СОЛНЕЧНОЙ СИСТЕМЕ. ГОРИЗОНТАЛЬНЫЙ ПАРАЛЛАКС (ВОРОНЦОВ-ВЕЛЬЯМИНОВ, 10-11 КЛАСС)
Земля
Её радиус
Её объем
150 млн км
350 млн км
Угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения
Изменение координат звезды, вызванное изменением положения наблюдателя из-за обращения Земли вокруг Солнца
Расстоянию от Земли до Солнца
250 млн км
меньше его параллакс
Нет верного ответа
Средство определения расстояния до тел солнечной системы
Это явление на планете Венера
2. В каком веке был определен горизонтальный параллакс?
Её радиус
Угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения
меньше его параллакс
150 млн км
Расстоянию от Земли до Солнца
Средство определения расстояния до тел солнечной системы
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс профессиональной переподготовки
География: теория и методика преподавания в образовательной организации
Курс профессиональной переподготовки
Методическая работа в онлайн-образовании
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-1207151
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Создана Ассоциация руководителей школ России и Беларуси
Время чтения: 1 минута
Каждый третий российский школьник хотел бы стать разработчиком игр
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Утверждены сроки заключительного этапа ВОШ
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Минпросвещения сформирует новый федеральный перечень учебников
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Конспект урока и презентация по астрономии 11 класс «Методы определения расстояний и размеров тел Солнечной системы»
План- конспект урока.
Учитель : Живаго О.И.
Учебник: Астрономия. Базовый уровень 11 класс. Учебник : М.: Дрофа. 2018.
Автор: Б.А.Воронцов-Вельяминов, Е.К.Страут.
Урок № 11 Дата: 21.11.2019 г
Тема урока: Определение расстояний и размеров тел в Солнечной системе.
Тип урока: урок открытия новых знаний.
Личностные: организовать самостоятельную познавательную деятельность; высказывать убежденность в единстве методов изучения параметров Земли и других планет.
Метапредметные : анализировать информацию. Полученную из текста научного содержания; объяснять суть эмпирического способа определения размеров Земли.
Предметные : формулировать определения терминов и понятий «горизонтальный параллакс», «угловые размеры объекта»; пояснять сущность метода определения расстояний по параллаксам светил, радиолокационного метода и метода лазерной локации; вычислять расстояния до планет по горизонтальному параллаксу, а их размеры по угловым размерам и расстоянию.
Изучить методы определения расстояний до небесных тел Солнечной системы.
2. Изучить методы определения размеров небесных тел:
— эмпирический способ Эратосфена (до н.э.);
— современные методы измерения размеров небесных тел.
3. Сравнить полученные результаты, полученные разными методами.
Оборудование: персональный компьютер, телевизор, Ресурс сети Интернет, презентация «определение расстояний и тел Солнечной системы», «Радиолокационный метод», « Вклад советских ученых в дело Победы», «Движение планеты Меркурий по диску Солнца».
Организационный этап. Мотивация.
Актуализация знаний. Проверка домашнего задания.
Изучение нового материала.
Закрепление изученного материала.
Рефлексия (рассуждения, беседа).
Подведение итога урока.
Приветствие. Проверка наличия учебных принадлежностей на столах.
Праздник учрежден 17 декабря 1996 года Генеральной Ассамблеей Организации
Объединенных Наций (ООН).
Остается добавить, что телевидению принадлежит важная роль в развитии общества.
Определение целей и задач урока.
(обучающиеся формулируют, учитель корректирует)
Проверка пройденного материала по теме: «Движение планет Солнечной системы»:
Тест-контроль (1 минута) (Приложение):
подчеркнуть правильный ответ;
критерии оценивания теста;
фронтальный опрос обучающихся, выполнивших тест;
Актуализация знаний. Проверка домашнего задания:
Сформулировать законы Иоганна Кеплера:
— Формулирует 1-й закона Кеплера:
1. Каждая планета обращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.
2. Радиус-вектор планеты за равные промежутки времени описывает равные площади.
3. Квадраты звёздных периодов обращения планет относятся между собой как кубы больших полуосей их орбит.
Границы применимости и в чем значимость законов Кеплера?
Задание 1. Заполнить таблицу (работа в паре) (смотри Приложение)
Воспользуйтесь данными приложения VI стр. 219 учебника., проверить результаты.
Вопрос: Что такое эксцентриситет?
Эксцентриситет равен отношению расстояния от центра эллипса до его фокуса к большой полуоси.
Предполагаемое решение: Так как эксцентриситет орбиты планеты равен нулю, то форма орбиты – окружность. Следовательно, малая полуось тоже равна 2,8 а.е.
Вопрос: Ребята, а какое астрономическое явление астрономы наблюдали совсем недавно? Такое явление происходит 13 раз за 100 лет.
Презентация: «Движение планеты Меркурий по диску Солнца».
Вопрос: Какое научное значение имеет наблюдение движения планет по диску Солнца?
Эти наблюдения сыграли очень важную роль в истории человечества, помогая совершить прорыв в астрономии.
Так как Меркурий и Венера находятся дальше от нас, чем Луна, они видны как небольшое пятно на поверхности Солнца.
Это пятно движется по диску солнца и если сделать серию фотографий во время прохождения, затем совместить их, то можно четко увидеть траекторию движения планеты.
За то время, когда внутренняя планета проходит по диску Солнца, астрономы пытаются определить состав атмосферы, температуру.
В среднем наблюдение Меркурия по диску Солнца наблюдается 13 раз за 100 лет и описывается очень сложными законами.
Предпоследнее прохождение планеты – 9 мая 2016 года
Последнее – 11 ноября 2019 года
Следующее – 7 мая 2049 года.
Изучение нового материала:
Сегодня на уроке мы рассмотрим другие методы определения расстояний до небесных тел и определение их размеров. Мы узнаем методы определения формы и размеров Земли. Зная расстояния, можно говорить о природе небесных тел:
— определять размеры не только Солнечной системы, но и больших объектов: Галактик, видимой части Вселенной;
— в определенной мере можно обеспечить безопасность окружающего пространства Земли,
— отслеживать приближение крупных астероидов;
— проводить расчеты для полетов космических аппаратов.
Задание: работа с текстом учебника.
Первые сведения об определении размеров Земли относятся к работам Эратосфена.
Вопрос: Кто такой Эратосфен?
Греческий ученый, жил в Египте. (276-194 г до н.э.)
Используя материал параграфа 13, п. 1, заполните пропуски в приведенном научном тексте, который лежит у вас на столе.
Стр. 64 – 65. Работаем самостоятельно. ( 5 мин)
Проверка выполненной работы.
Методы определения расстояний в Солнечной системе (на доске) :
Метод лазерной локации.
Астрономические понятия (записываем в тетрадь):
Параллактическое смещение – изменение направления на предмет при перемещении наблюдателя. (Учебник стр. 66, рис. 3.9)
Параллакс – угол, под которым виден радиус Земной орбиты.
1. Метод горизонтального параллакса: (Просмотр слайдов. Презентация: «Определение расстояний и размеров тел в Солнечной системе»)
Горизонтальный параллакс – угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения. (Учебник стр. 68)
Вывод: Чем дальше расположен объект, тем меньше его параллакс.
В настоящее время благодаря использованию лазеров стало возможным проводить оптическую локацию Луны с точностью до 1 см.
Ребята, 2020 год – Год памяти и славы в ознаменование 75-летия Победы в ВОВ.
Успешное использование радиолокаторов для обнаружения движущихся военных объектов – самолетов, кораблей – сыграло огромную роль в военном деле и способствовало нашей Победе в годы ВОВ. Нам нужно знать и помнить о большом вкладе советских ученых, конструкторов в дело Победы 1945 года.
Закрепление изученного материала:
Какие измерения, выполненные на Земле, свидетельствуют о ее сжатии?
Каким методом определяется расстояние до ближайших планет в настоящее время?
Задача : (Решают в тетрадях и 1 ученик у доски)
Через сколько времени воображаемый наблюдатель зафиксирует солнечную вспышку на Юпитере. Если на Земле ее зафиксировали чере 8,3 мин после появления.
Ребята, вернитесь к записям сегодняшнего урока, подумайте, что для вас сегодня было новым, интересным.
Продолжая фразу по очереди, начиная с 1 парты:
— Сегодня я узнал ….
— Мне было интересно …
Обучающиеся подводят итоги, определяют, каких результатов они достигли.
6. Домашнее задание: Изучить параграф 13, вопросы, упр.11 (1-3).
Темы для проектной деятельности:
Современные методы геодезических измерений.
Определение расстояний в Солнечной системе. Горизонтальный параллакс
Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является её радиус.
Горизонтальным параллаксом (р) называется угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения (рис. 3.11).
Из треугольника OAS можно выразить величину — расстояние OS = D:
где R — радиус Земли. По этой формуле можно вычислить расстояние в радиусах Земли, а зная его величину, — выразить расстояние в километрах.
Очевидно, что чем дальше расположен объект, тем меньше его параллакс. Наибольшее значение имеет параллакс Луны, который меняется в связи с тем, что Луна обращается по эллиптической орбите, и в среднем составляет 57′. Параллаксы планет и Солнца значительно меньше. Так, параллакс Солнца равен 8,8″. Такому значению параллакса соответствует расстояние до Солнца, примерно равное 150 млн км. Это расстояние принимается за одну астрономическую единицу (1 а. е.) и используется при измерении расстояний между телами Солнечной системы.
Известно, что для малых углов sin р ≈ р, если угол р выражен в радианах. В одном радиане содержится 206 265″. Тогда, заменяя sin р на р и выражая этот угол в радианной мере, получаем формулу в виде, удобном для вычислений:
или (с достаточной точностью)
Во второй половине XX в. развитие радиотехники позволило определять расстояния до тел Солнечной системы посредством радиолокации. Первым объектом среди них стала Луна. Затем радиолокационными методами были уточнены расстояния до Венеры, Меркурия, Марса и Юпитера. На основе радиолокации Венеры величина астрономической единицы определена с точностью порядка километра. Столь высокая точность определения расстояний — необходимое условие для расчётов траекторий полёта космических аппаратов, изучающих планеты и другие тела Солнечной системы. В настоящее время благодаря использованию лазеров стало возможным провести оптическую локацию Луны. При этом расстояния до лунной поверхности измеряются с точностью до сантиметров.