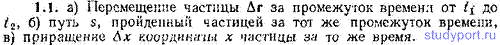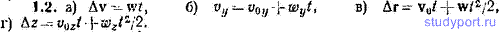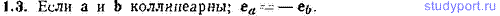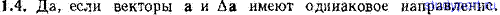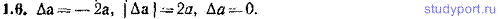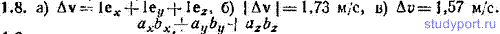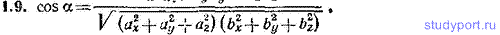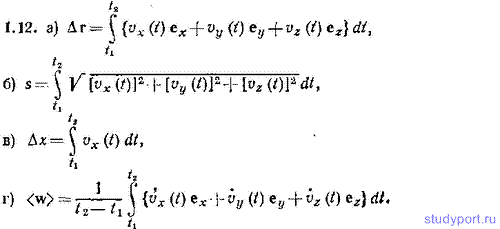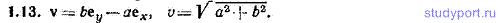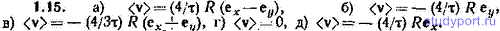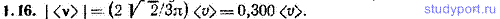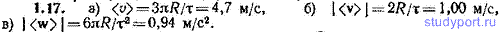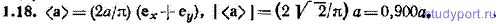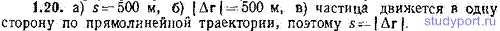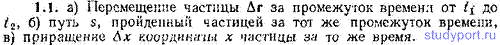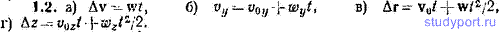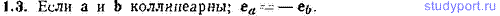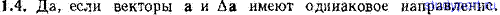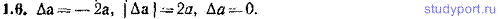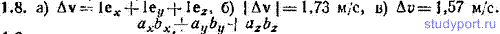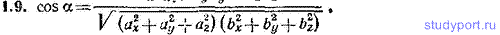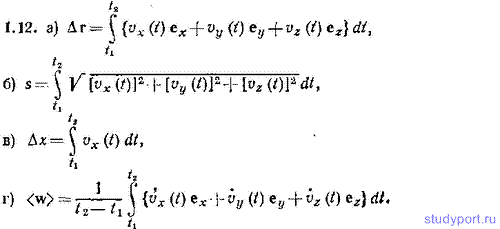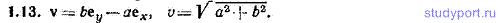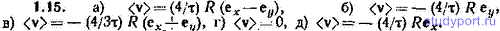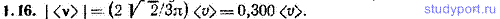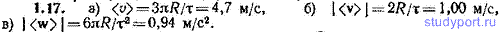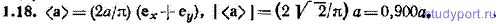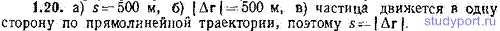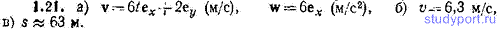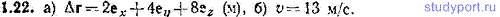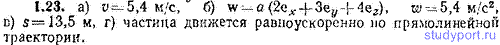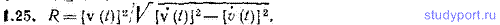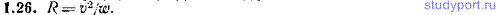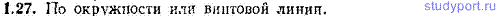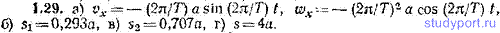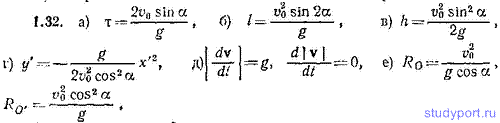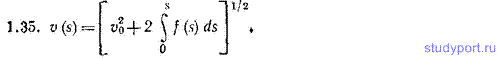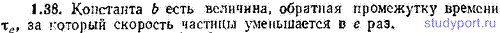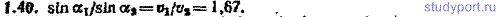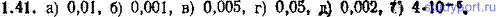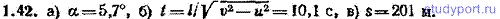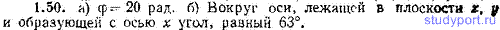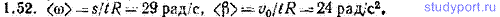Частица движется с постоянной скоростью v что определяет выражение
Кинематика
1.1. Частица движется с постоянной скоростью v. Что определяет выражение: a) v(t2-t1), б) v(t2-t1), в) vx(t2-t1)?
1.2. Частица движется с постоянным ускорением w. В начальный момент времени она находилась в точке с радиус-вектором r0 и имела скорость v0. Написать выражение для: а) приращения скорости частицы dv за время t, б) проекции скорости частицы на ось у в момент времени t, в) перемещения частицы за время t, г) приращения координаты z частицы за время.
1.4. Может ли приращение модуля вектора Δа оказаться равным модулю приращения вектора |Δа|?
1.5. В каком соотношении находятся приращение модуля вектора и модуль приращения вектора |Δа|, если векторы а и Δа направлены в противоположные стороны?
1.6. Вектор а изменил направление на обратное. Найти: Δa, |Δa|, Δa.
1.7. Вектор а повернулся без изменения «длины» на малый угол δφ. а) Написать приближенное выражение для |Δа|. б) Чему равно Δа?
1.8. Начальное значение скорости равно v1=1ex+3ey+5ez (м/с), конечное v2=2ex+4ey+6ez (м/с). Найти: а) приращение скорости Δv, б) модуль приращения скорости |Δv|, в) приращение модуля скорости Δv.
1.9. Написать выражение для косинуса угла α между векторами с компонентами ax, ay, az и bx, by, bz.
1.11. Преобразовать к виду, содержащему только модули векторов и угол α, выражение a [bc], в котором векторы а и с взаимно перпендикулярны, а вектор b образует с нормалью к плоскости, в которой лежат векторы а и с, угол α.
1.12. Заданы функции vx(t), vy(t) и vz(t), определяющие в некоторой системе координат скорость частицы v. Написать выражение для: а) перемещения частицы Δr за промежуток времени от t1 до t2, б) пути s, пройденного частицей за тот же промежуток времени, в) приращения Δх координаты х частицы за время от t1 до t2. г) среднего значения ускорения частицы за то же время.
1.13. Частица 1 движется со скоростью v1 = aex, частица 2 — со скоростью v2=bey (a и b — константы). Найти скорость v второй частицы относительно первой и модуль v этой скорости.
1.15. Частица движется равномерно по часовой стрелке по окружности радиуса R, делая за время τ один оборот. Окружность лежит в координатной плоскости x, y, причем центр окружности совпадает с началом координат. В момент t = 0 частица находится в точке с координатами x = 0, y = R. Найти среднее значение скорости точки за промежуток времени: а) от 0 до τ/4, б) от 0 до τ/2, в) от 0 до 3τ/4, г) от 0 до τ, д) от τ/4 до 3τ/4.
1.16. Частица прошла за некоторое время 3/4 окружности со средним значением модуля скорости (v). Найти модуль средней скорости частицы | | за то же время.
1.18. Постоянный по модулю вектор а, равномерно поворачиваясь против часовой стрелки в плоскости х, у, переходит за время из положения, при котором он совпадает по направлению с осью х, в положение, при котором он совпадает по направлению с осью у. Найти среднее за время значение вектора а и модуль этого среднего.
1.19. Радиус-вектор точки r изменяется: а) только по модулю, б) только по направлению. Что можно сказать о траектории?
1.20. Радиус-вектор частицы определяется выражением: r=3t 2 ex+4t 2 ey+7ez (м). Вычислить: а) путь s, пройденный частицей за первые 10 секунд движения, б) модуль перемещения |Δr| за то же время, в) объяснить полученные результаты.
Ошибка в тексте? Выдели её мышкой и нажми
1.1. Частица движется с постоянной скоростью v. Что определяет выражение: a) v(t2-t1), б) v(t2-t1), в) vx(t2-t1)?
1.2. Частица движется с постоянным ускорением w. В начальный момент времени она находилась в точке с радиус-вектором r0 и имела скорость v0. Написать выражение для: а) приращения скорости частицы dv за время t, б) проекции скорости частицы на ось у в момент времени t, в) перемещения частицы за время t, г) приращения координаты z частицы за время.
1.4. Может ли приращение модуля вектора Δа оказаться равным модулю приращения вектора |Δа|?
1.5. В каком соотношении находятся приращение модуля вектора и модуль приращения вектора |Δа|, если векторы а и Δа направлены в противоположные стороны?
1.6. Вектор а изменил направление на обратное. Найти: Δa, |Δa|, Δa.
1.7. Вектор а повернулся без изменения «длины» на малый угол δφ. а) Написать приближенное выражение для |Δа|. б) Чему равно Δа?
1.8. Начальное значение скорости равно v1=1ex+3ey+5ez (м/с), конечное v2=2ex+4ey+6ez (м/с). Найти: а) приращение скорости Δv, б) модуль приращения скорости |Δv|, в) приращение модуля скорости Δv.
1.9. Написать выражение для косинуса угла α между векторами с компонентами ax, ay, az и bx, by, bz.
1.11. Преобразовать к виду, содержащему только модули векторов и угол α, выражение a [bc], в котором векторы а и с взаимно перпендикулярны, а вектор b образует с нормалью к плоскости, в которой лежат векторы а и с, угол α.
1.12. Заданы функции vx(t), vy(t) и vz(t), определяющие в некоторой системе координат скорость частицы v. Написать выражение для: а) перемещения частицы Δr за промежуток времени от t1 до t2, б) пути s, пройденного частицей за тот же промежуток времени, в) приращения Δх координаты х частицы за время от t1 до t2. г) среднего значения ускорения частицы за то же время.
1.13. Частица 1 движется со скоростью v1 = aex, частица 2 — со скоростью v2=bey (a и b — константы). Найти скорость v второй частицы относительно первой и модуль v этой скорости.
1.15. Частица движется равномерно по часовой стрелке по окружности радиуса R, делая за время τ один оборот. Окружность лежит в координатной плоскости x, y, причем центр окружности совпадает с началом координат. В момент t = 0 частица находится в точке с координатами x = 0, y = R. Найти среднее значение скорости точки за промежуток времени: а) от 0 до τ/4, б) от 0 до τ/2, в) от 0 до 3τ/4, г) от 0 до τ, д) от τ/4 до 3τ/4.
1.16. Частица прошла за некоторое время 3/4 окружности со средним значением модуля скорости (v). Найти модуль средней скорости частицы | | за то же время.
1.18. Постоянный по модулю вектор а, равномерно поворачиваясь против часовой стрелки в плоскости х, у, переходит за время из положения, при котором он совпадает по направлению с осью х, в положение, при котором он совпадает по направлению с осью у. Найти среднее за время значение вектора а и модуль этого среднего.
1.19. Радиус-вектор точки r изменяется: а) только по модулю, б) только по направлению. Что можно сказать о траектории?
1.20. Радиус-вектор частицы определяется выражением: r=3t 2 ex+4t 2 ey+7ez (м). Вычислить: а) путь s, пройденный частицей за первые 10 секунд движения, б) модуль перемещения |Δr| за то же время, в) объяснить полученные результаты.
1.21. Радиус-вектор частицы изменяется со временем по закону: r=3t 2 ex+2tey+1ez (м). Найти: а) скорость v и ускорение w частицы, б) модуль скорости v в момент t=1 с, в) приближенное значение пути s, пройденного частицей за 11-ю секунду движения.
1.22. Частица движется со скоростью v=1ex+2tey+3t 2 ez (м/с). Найти: а) перемещение Δr частицы за первые 2 секунды ее движения, б) модуль скорости v в момент t=2 с.
1.23. Частица движется со скоростью v=at(2ex+3ey+4ez) (a =1,00 м/с 2 ). Найти: а) модуль скорости v частицы в момент времени t=1,00 с, б) ускорение частицы w и его модуль w, в) путь s, пройденный частицей с момента t1=2,00 с до момента t2=3,00 с, г) какой характер имеет движение частицы.
1.25. Известна функция v(t) для частицы, движущейся по криволинейной траектории. Написать выражение для радиуса кривизны R траектории в той точке, в которой частица находится в момент t?
1.26. Частица движется равномерно по криволинейной траектории. Модуль ее скорости равен v. Найти радиус кривизны R траектории в той точке, где модуль ускорения частицы равен w.
1.27. По какой траектории движется частица в случае, если ωτ = 0, ωn = const?
1.29. Точка движется вдоль оси x, причем координата x изменяется по закону x=a cos(2π/T)t. Найти: а) выражения для проекций на ось х скорости v и ускорения w точки, б) путь s1, пройденный точкой за промежуток времени от t=0 до t=T/8, в) путь s2, пройденный точкой за промежуток времени от t=T/8 до t=T/4, г) путь s, пройденный точкой за промежуток времени от t=0 до t=T.
1.30. Компоненты скорости частицы изменяются со временем по законам: vx=a cos ωt, vy=a sin ωt, vz=0, где а и ω — константы. Найти модули скорости v и ускорения w, а также угол α между векторами v и w. На основании полученных результатов сделать заключение о характере движения частицы.
1.31. Зависимость координат движения частицы от времени имеет вид x=a cos ωt, y=a sin ωt, z=0 (а и ω — константы). а) Определить радиус-вектор r, скорость v и ускорение w частицы, а также их модули. б) Вычислить скалярное произведение векторов r и v. Что означает полученный результат? в) Вычислить скалярное произведение векторов r и w. Что означает полученный результат? г) Найти уравнение траектории частицы. д) В каком направлении движется по траектории частица? е) Охарактеризовать движение частицы. ж) Как изменится движение частицы, если в выражении для y изменить знак на обратный?
1.32. Небольшое тело (материальная точка) брошено из точки О под углом α к горизонту с начальной скоростью v0 (рис. 1.1). Пренебрегая сопротивлением воздуха, найти: а) время полета τ, б) дальность полета l, в) наибольшую высоту поднятия тела h, г) уравнение траектории тела в координатах x’, y’, д) значения |dv/dt| и d|v|/dt в вершине траектории, е) радиус кривизны R траектории в точках О и О’. Точки бросания и падения считать лежащими на одном уровне.
1.33. Тело брошено под углом к горизонту с начальной скоростью v0. Пренебрегая сопротивлением воздуха, найти среднее значение скорости за первые τ секунд полета.
1.35. Известны: функция f(s), определяющая зависимость производной dv/dt от пройденного частицей пути s, модуль скорости v0 в начале пути. Написать выражение для v(s) — модуля скорости, которую имеет частица, пройдя путь s.
1.36. Дана функция v(s), определяющая зависимость модуля скорости частицы от пройденного частицей пути s. Написать выражение для времени t, затрачиваемого частицей на прохождение пути s.
1.40. Ось x на рис. 1.2 служит границей между участком, поросшим травой, и участком, покрытым рыхлым песком. Пешеходу нужно попасть из пункта А в пункт В. По траве пешеход может идти со скоростью v1=5,00 км/ч, по песку — со скоростью v2=3,00 км/ч. Чтобы совершить переход за самое короткое время, пешеход выбирает ломаный путь АОВ. При каком соотношении между синусами углов α1 и α2 время движения пешехода из A в B будет минимальным?
1.43. Имеются две моторные лодки, развивающие относительно воды скорость v = 5,00 м/с. Вода течет с одинаковой по всей ширине реки скоростью v = 0,500 м/с. Ширина реки l = 1 км. На середине реки вбиты две сваи С и D, отстоящие друг от друга на расстояние, равное ширине реки l (рис 1.4). Одной лодке нужно пересечь реку строго в поперечном направлении из точки А в точку В и обратно. Второй лодке нужно проделать путь от сваи С до сваи D и обратно. а) Как должна двигаться первая лодка относительно воды, чтобы относительно, берегов перемещаться вдоль прямой АВ? б) Найти времена t1 и t2, затрачиваемые на прохождение пути 2l первой и второй лодками. в) Получить для t1 и t2 приближенные выражения, справедливые для u 2 ex и ω2 = 2at 2 ey. а) На какой угол φ повернется тело за первые 3,00 с? б) Вокруг какой оси произойдет этот поворот?
1.52. До начала торможения автомобиль имел скорость v0 = 60 км/ч. После начала торможения автомобиль двигался прямолинейно с непостоянным ускорением и остановился спустя время t = 3,00 с. За это время он прошел путь s = 20,0 м. Определить среднюю угловую скорость и среднее угловое ускорение колеса автомобиля за время торможения. Радиус колеса R = 0,23 м.
1.53. Частица движется по радиусу вращающегося диска со скоростью v = 3.00 м/с. В начальный момент времени частица находится в центре диска. Угловая скорость вращения диска ω = 20,0 рад/с. Найти приближенное значение пути s, пройденного частицей в неподвижной системе отсчета за время с момента t1 = 9,00 с до момента t2 = 10,00 с.
Ответы на все модули (для контрольного теста) по предмету физика
Ответы на все модули (для контрольного теста) по предмету физика.
Ответы на модуль 1 (ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ) по предмету физика.
1) Выберите формулу для расчета первой космической скорости.
2) К ободу диска массой m = 5 кг приложена касательная сила F = 19,6 Н. Какую кинетическую энергию будет иметь диск через время t = 5 c после начала действия силы?
3) Какая из приведенных размерностей соответствует мощности?
4) Как называется минимальная скорость, которую надо сообщить ракете, чтобы она могла упасть в заданную точку Солнца?
четвертая космическая скорость
7) Какая из приведенных ниже формул выражает связь между линейной и угловой скоростью?
8) Какая из приведенных ниже формул выражает закон сохранения механической энергии?
9) Выберите формулу для расчета момента инерции тела относительно произвольной оси.
10) Что определяет формула V=….
минимальное значение третьей космической скорости
11) Какая из приведенных ниже формул является математическим выражением закона всемирного тяготения?
12) Какая из приведенных ниже формул выражает связь между параболической и круговой скоростью планеты?
14) Какая из приведенных ниже формул выражает основной закон динамики вращательного движения твердого тела относительно неподвижной оси?
15) Выберите формулу для расчета модуля ускорения материальной точки, движущейся по криволинейной траектории?
16) Какова величина гравитационной постоянной?
19) Укажите уравнение динамики поступательного движения материальной точки.
20) Для каких систем отсчета справедлив первый закон Ньютона?
для инерциальных систем отсчета
21) Мальчик катит обруч по горизонтальной дороге со скоростью v = 2 м/с. На какую высоту H может вкатиться обруч на горку за счет своей кинетической энергии?
22) Пуля массой m = 20 г, летящая с горизонтальной скоростью v = 500 м/с, попадает в мешок с песком массой M = 5 кг, висящий на длинном шнуре, и застревает в нем. Найти высоту H, на которую поднимется мешок.
23) Найти радиус R вращающегося колеса, если известно, что линейная скорость точки, лежащей на ободе, в 2,5 раза больше линейной скорости точки, лежащей на расстоянии r = 5 cм ближе к оси колеса.
24) Какова величина второй космической скорости?
Ответы на модуль 2 (ОСНОВЫ РЕЛЯТИВИСТСКОЙ МЕХАНИКИ) по предмету физика.
1) Как формулируется второй постулат теории относительности Эйнштейна?
скорость света в вакууме не зависит от движения источника и приемника света и, следовательно, одинакова во всех инерциальных системах отсчета
2) Какой вид имеют преобразования Лоренца в случае, когда сходственные оси декартовых координат неподвижной К и движущейся К’ инерциальных систем попарно параллельны, система отсчета К’ движется относительно К с постоянной скоростью v вдоль оси ОХ, за начало отсчета времени в обеих системах выбран тот момент, когда начала координат обеих систем совпадают (t = 0 и t’ = 0)?
3) Определить относительную скорость движения, при которой релятивистское сокращение линейных размеров тела составляет 10%.
4) Определить релятивистский импульс протона, если скорость его движения v = 0,8с.
5) Определить релятивистский импульс р электрона, движущегося со скоростью v = 0,9с (где с — скорость света в вакууме).
6) С космического корабля, удаляющегося от Земли со скоростью 0,75с, стартует ракета в направлении движения корабля. Скорость ракеты относительно Земли 0,96с. Какова скорость ракеты относительно корабля?
7) Электрон движется со скоростью v = 0,6с. Определить релятивистский импульс р электрона.
8) Что определяет формула W=…..
релятивистское правило сложения скоростей
9) Как формулируется первый постулат теории относительности Эйнштейна?
никакими измерениями в произвольной системе отсчета нельзя обнаружить ее прямолинейное и равномерное движение, то есть все процессы, происходящие в системе, не зависят от ее прямолинейного и равномерного движения
10) Полная энергия тела возросла на ΔЕ = 1 Дж. На сколько при этом изменится масса тела?
11) Выберите формулу для расчета релятивистской массы тела.
12) Какая из приведенных ниже формул выражает релятивистское сокращение длины?
13) Какая из приведенных ниже формул выражает релятивистское замедление времени?
14) Частица движется со скоростью v = 0,5с. Во сколько раз релятивистская масса частицы больше массы покоя?
15) Два автомобиля движутся в одном и том же направлении со скоростями и относительно поверхности Земли. Чему равна скорость света фар первого автомобиля в системе отсчета, связанной с другим автомобилем?
16) Полная энергия релятивистской частицы в 8 раз превышает ее энергию покоя. Определить скорость этой частицы.
17) На сколько процентов релятивистская масса частицы больше массы покоя при скорости v = 30 Мм/с?
18) На примере каких элементарных частиц наблюдается эффект замедления времени в движущихся часах с точки зрения неподвижного наблюдателя?
19) В лабораторной системе отсчета удаляются друг от друга две частицы с одинаковыми по модулю скоростями. Их относительная скорость и в той же системе отсчета равна 0,5с. Определить скорости частиц.
20) С какой скоростью должна лететь ракета, чтобы время в ней замедлялось в три раза?
21) Какая из приведенных ниже формул выражает соотношение между релятивистской массой и механической энергией?
22) Во сколько раз увеличится масса частицы при движении со скоростью 0,5с?
23) В ракете, движущейся со скоростью 0,96с, было зафиксировано время полета 1 год. Сколько времени должно пройти по подсчетам земного наблюдателя?
24) С какой скоростью должен двигаться электрон, чтобы его масса в состоянии движения увеличилась на 100%?
25) Фотонная ракета движется относительно Земли со скоростью v = 0,6с. Во сколько раз замедлится ход времени в ракете с точки зрения земного наблюдателя?
Ответы на модуль 3 (МОЛЕКУЛЯРНАЯ ФИЗИКА. КИНЕМАТИКА И ДИНАМИКА ЖИДКОСТЕЙ И ГАЗОВ) по предмету физика.
1) Каков физический смысл уравнения Бернулли?
в установившемся потоке идеальной несжимаемой жидкости полное давление, слагаемое из динамического, гидравлического и статического, постоянно на любом поперечном сечении потока
3) Какое количество вещества содержится в 8 г водорода?
7) По какой формуле определяется вязкость газа?
8) Чему равен абсолютный нуль температуры, выраженный по шкале Цельсия?
9) Какое выражение, приведенное ниже, соответствует барометрической формуле?
10) Относительная молекулярная масса гелия равна 4. Выразите в кг/моль молярную массу гелия.
11) Определить концентрацию n молекул газа, содержащегося в колбе вместимостью при температуре T = 290 К и давлении p = 50 кПа.
12) Найти среднюю длину свободного пробега λ молекул углекислого газа при температуре t = 100° С и давлении р = 13,3 Па. Диаметр молекул углекислого газа σ = 0,32 нм.
распределение относительного числа молекул газа по скоростям в состоянии равновесия
14) Найти коэффициент диффузии D воздуха при давлении р = 101,3 кПа и температуре t = 10° С. Диаметр молекул воздуха σ = 0,3 нм.
16) Определить количество вещества ν молекул азота массой m = 0,2 кг.
17) Укажите основное уравнение кинетической теории газов.
18) Какому значению числа Рейнольдса соответствует турбулентное движение жидкости?
20) Какое выражение, приведенное ниже, соответствует формуле Стокса?
21) Укажите уравнение Бернулли.
22) Какое выражение, приведенное ниже, соответствует формуле количества вещества?
23) Сколько молекул находится в одном грамме воды?
24) Какому значению числа Рейнольдса соответствует ламинарное движение жидкости?
Ответы на модуль 4 (ОСНОВЫ ТЕРМОДИНАМИКИ. РЕАЛЬНЫЕ ГАЗЫ, ЖИДКОСТИ И ТВЕРДЫЕ ТЕЛА) по предмету физика.
3) Выберите формулу для расчета энергии Гиббса.
4) При каких условиях применимо уравнение Ван-дер-Ваальса?
5) Какую температуру Т имеет масса m = 2 г азота, занимающего объем при давлении р = 0,2 МПа?
6) Как формулируется правило фаз Гиббса?
для обеспечения равновесия многофазной системы необходимо, чтобы число фаз было равно или меньше числа компонент плюс два, то есть r ≤ n + 2
7) Укажите уравнение Ван-дер-Ваальса.
10) Укажите уравнение первого закона термодинамики для системы с переменной массой.
11) При изотермическом расширении массы m = 10 г азота, находящегося при температуре t = 17°С, была совершена работа А = 860 Дж. Во сколько раз изменилось давление азота при расширении?
12) Выберите формулу для расчета внутренней энергии газа Ван-дер-Ваальса для случая, когда зависимостью теплоемкости от температуры можно пренебречь.
14) Как называется отношение абсолютной влажности ненасыщенного влажного воздуха к максимально возможной при данной температуре?
относительная влажность воздуха
15) Как называется равновесное сосуществование нескольких соприкасающихся между собой различных фаз вещества?
16) Выберите формулу для расчета высоты поднятия или опускания жидкости в капилляре.
17) Выберите формулу для расчета энтропии.
18) Как называется переход вещества из твердой фазы в газообразную?
19) Найти удельную теплоемкость с кислорода для V = const, р = const.
20) Какое выражение, приведенное ниже, соответствует изменению внутренней энергии идеального газа в любом термодинамическом процессе?
21) Выберите формулу для расчета осмотического давления.
23) Среди приведенных ниже формул найдите ту, по которой вычисляется термический коэффициент полезного действия.
24) Какая из приведенных ниже формул определяет избыточное давление, создаваемое силами натяжения на произвольной поверхности жидкости двоякой кривизны?
25) Масса m = 12 г азота, находится в закрытом сосуде объемом V = 2 л, при температуре t = 10° С. После нагревания давление в сосуде стало равным р = 1,33 МПа. Какое количество теплоты Q сообщено газу при нагревании?
Ответы на модуль 5 (ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК) по предмету физика.
1) Какая из приведенных ниже формул выражает закон Ома в дифференциальной форме?
2) Лампочка и реостат, соединенные последовательно, присоединены к источнику тока. Напряжение U на зажимах лампочки равно 40 В, сопротивление R реостата равно 10 Ом. Внешняя цепь потребляет мощность Р = 120 Вт. Найти силу тока I в цепи.
4) Какая из приведенных ниже формул выражает закон Джоуля-Ленца?
5) Какая из приведенных ниже формул выражает закон Ома для участка цепи?
6) Определить напряженность E электрического поля, создаваемого точечным зарядом Q = 10 нКл на расстоянии r = 10 см от него. Диэлектрик — масло.
напряженность электростатического поля в фиксированной точке
8) Как называются твердые диэлектрики, способные после прекращения действия внешнего электрического поля длительно (от нескольких дней до миллионов лет) сохранять поляризованное состояние?
9) Какая из приведенных ниже формул выражает теорему Остроградского-Гаусса?
11) Выберите формулу для расчета электроемкости плоского конденсатора.
диэлектрическая восприимчивость вещества
14) Выберите формулу для расчета удельного электрического сопротивления.
15) Расстояние между двумя точечными зарядами и равно 10 см. Определить силу F, действующую на точечный заряд Q = 0,l мкКл, удаленный на от первого и на см от второго зарядов.
16) Какая из приведенных ниже формул выражает закон Ома для замкнутой цепи?
18) Как называются диэлектрики с высоким значением диэлектрической проницаемости?
19) Поле создано точечным зарядом Q = 1 нКл. Определить потенциал φ поля в точке, удаленной от заряда на расстояние r = 20 см.
21) Плоский конденсатор заряжен до разности потенциалов U = 1 кВ. Расстояние d между пластинами равно 1 см. Диэлектрик — стекло. Определить объемную плотность энергии поля конденсатора.
22) Какая из приведенных ниже формул выражает закон Кулона для изотропной диэлектрической среды?
23) Какая формула выражает зависимость удельного сопротивления проводника от температуры?
24) Какая из приведенных размерностей соответствует поверхностной плотности заряда?
25) Чему равна масса вещества, оседающего на электроде, при электролизе?
Ответы на модуль 6 (МАГНИТОСТАТИКА. МАГНИТНОЕ ПОЛЕ) по предмету физика.
1) Выберите формулу для расчета магнитной индукции в центре кругового проводника с током.
2) Электрон, пройдя ускоряющую разность потенциалов U = 400 В, попал в однородное магнитное поле с индукцией В = 1,5 мТл. Определить радиус R кривизны траектории.
3) Какие из приведенных ниже формул выражают систему уравнений Максвелла в интегральной форме?
4) По прямому бесконечно длинному проводнику течет ток I = 50 А. Определить магнитную индукцию В в точке, удаленной на расстояние r = 5 см от проводника.
5) Выберите формулу для расчета силы, действующей на проводник с током в магнитном поле.
6) Как называется явление, заключающееся в том, что в проводнике с током плотностью помещенном в магнитное поле с индукцией возникает разность потенциалов в направлении, перпендикулярном векторам вследствие действия силы Лоренца на заряды, движущиеся упорядочено в проводнике со средней скоростью
7) Найти магнитную индукцию в центре тонкого кольца, по которому идет ток I = 10 А. Радиус r кольца равен 5 см.
8) Как называется свойство многих проводников, состоящее в том, что их электрическое сопротивление скачком падает до нуля при охлаждении ниже определенной критической температуры, характерной для данного материала?
9) Каково значение магнитной проницаемости для ферромагнетиков?
10) По двум параллельным прямым проводам длиной l = 2,5 м каждый, находящимся на расстоянии d = 20 см друг от друга, текут одинаковые токи I = 1 кА. Вычислить силу F взаимодействия токов.
11) Каково значение электрической постоянной?
12) Каково значение магнитной постоянной?
13) Напряженность Н магнитного поля равна 79,6 кА/м. Определить магнитную индукцию В этого поля в вакууме.
14) Какая из приведенных размерностей соответствует магнитной индукции?
15) Какая формула выражает связь между векторами магнитной индукции и напряженности для однородной изотропной среды?
16) Определить силу Лоренца F, действующую на электрон, влетевший со скоростью V = 4 Мм/с в однородное магнитное поле под углом α = 30° к линиям индукции. Магнитная индукция В поля равна 0,2 Тл.
17) По соленоиду течет ток I = 2 А. Магнитный поток Ф, пронизывающий поперечное сечение соленоида, равен 4 мкВб. Определить индуктивность L соленоида, если он имеет N = 800 витков.
18) Электрон движется по окружности в однородном магнитном поле напряженностью H = 10 кА/м. Вычислить период Т вращения электрона.
19) Как называется возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока?
20) По двум бесконечно длинным прямым параллельным проводам текут токи и в противоположных направлениях. Расстояние d между проводами равно 20 см. Определить магнитную индукцию В в точке, удаленной на от первого и на см от второго провода.
21) По витку радиусом r = 5 см течет ток I = 10 А. Определить магнитный момент кругового тока.
22) Выберите формулу для расчета магнитной индукции прямого бесконечно длинного проводника.
23) Какие из приведенных ниже формул выражают систему уравнений Максвелла в дифференциальной форме?
24) Какая из приведенных ниже формул выражает закон Био-Савара-Лапласа?
25) Выберите формулу для расчета магнитной индукции для участка прямого проводника с током.
Ответы на модуль 7 (ФИЗИКА КОЛЕБАНИЙ И ВОЛН) по предмету физика.
1) Гармонические колебания величины s описываются уравнением Определить период колебаний.
2) Амплитуда затухающих колебаний маятника за t = 2 мин уменьшилась в 2 раза. Определить коэффициент затухания δ.
3) Укажите дифференциальное уравнение движения материальной точки массой m под действием упругой силы и силы трения.
4) Укажите дифференциальное уравнение гармонических колебаний.
5) В цепь колебательного контура, содержащего последовательно соединенные резистор сопротивлением R = 40 Ом, катушку индуктивностью L = 0,36 Гн и конденсатор емкостью С = 28 мкФ, подключено внешнее переменное напряжение с амплитудным значением и частотой ω = 314 рад/с. Определить амплитудное значение силы тока в цепи.
6) Какая из приведенных ниже формул выражает циклическую частоту пружинного осциллятора?
потенциальную составляющую энергии колебательного движения
кинетическую составляющую энергии колебательного движения
9) Укажите дифференциальное уравнение незатухающих электромагнитных колебаний.
10) Два одинаково направленных гармонических колебания одинакового периода с амплитудами и имеют разность фаз φ = 45°. Определить амплитуду результирующего колебания.
11) Точка совершает гармонические колебания с амплитудой А = 10 см и периодом Т = 5 с. Определить для точки максимальное ускорение.
полную энергию гармонического колебания
13) Каково соотношение частот при продольном эффекте Доплера в случае сближения?
14) Колебательный контур состоит из конденсатора емкостью С = 888 пФ и катушки с индуктивностью L = 2 мГн. На какую длину волны λ настроен контур?
15) Какую индуктивность L надо включить в колебательный контур, чтобы при емкости С = 2 мкФ получить частоту ν = 1000 Гц?
16) Каково соотношение частот при поперечном эффекте Доплера?
17) Как называется резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающего фактора к частоте резонансной?
18) Укажите уравнение движения пружинного маятника.
19) Какая из приведенных ниже формул выражает период свободных колебаний электрического контура?
20) Какая из приведенных ниже формул выражает период колебаний математического маятника?
21) Материальная точка массой m = 20 г совершает гармонические колебания по закону Определить полную энергию Е этой точки.
22) Укажите дифференциальное уравнение вынужденных колебаний.
23) Укажите уравнение распространения волн в изотропной среде.
24) Уравнение изменения со временем тока в колебательном контуре имеет вид Индуктивность контура L = 1 Гн. Найти максимальную энергию магнитного поля.
25) Точка совершает гармонические колебания с периодом Т = 6 с и начальной фазой, равной нулю. Определить, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.
Ответы на модуль 8 (ГЕОМЕТРИЧЕСКАЯ ОПТИКА И ФОТОМЕТРИЯ) по предмету физика.
1) В каком направлении пловец, нырнувший в воду, видит заходящее Солнце?
2) В полдень во время весеннего и осеннего равноденствия Солнце стоит на экваторе в зените. Во сколько раз в это время освещенность поверхности Земли на экваторе больше освещенности поверхности Земли в Ленинграде? Широта Ленинграда φ = 60°.
3) Какая из приведенных ниже формул выражает фазовую скорость света?
4) Как называется оптическая характеристика среды, которая показывает, во сколько раз фазовая скорость света в данной среде меньше скорости света в вакууме?
абсолютный показатель преломления
6) Как называется явление, при котором луч, падающий на границу раздела двух сред, полностью отражается, не проникая во вторую среду?
полное отражение света
7) На каких явлениях света основана работа стеклянных призм, используемых в оптических приборах?
полное отражение и преломление на границах призмы
9) Как называется отношение светового потока к величине телесного угла, в пределах которого этот световой поток распространяется?
10) Какой спектр характерен для нагретых твердых тел и жидкостей?
12) Как называется разложение света в спектр, происходящее при его преломлении?
13) Какой спектр характерен для нагретых одноатомных разреженных газов?
14) Какая из приведенных ниже формул выражает закон преломления?
15) На плоскопараллельную стеклянную (n = 1,5) пластинку толщиной l = 5 см падает под углом α = 30″ луч света. Определить боковое смещение луча, прошедшего сквозь эту пластинку.
16) Монохроматический луч падает на боковую поверхность прямоугольной равнобедренной призмы. Войдя в призму, луч претерпевает полное внутреннее отражение от основания призмы и выходит через вторую боковую поверхность призмы. Каким должен быть наименьший угол падения i луча на призму, чтобы еще происходило полное внутреннее отражение? Показатель преломления материала призмы для этого луча n = 1,5.
17) Какая из приведенных размерностей соответствует световому потоку?
18) 21 марта, в день весеннего равноденствия, на Северной Земле Солнце стоит в полдень под углом α = 10° к горизонту. Во сколько раз освещенность площадки, поставленной вертикально, будет больше освещенности горизонтальной площадки?
19) Укажите общую формулу линзы.
20) Как называется изменение направления световых лучей при изменении преломления показателя среды, через которую эти лучи проходят?
21) На лист белой бумаги перпендикулярно к поверхности падает световой поток Ф = 120 лм. Найти освещенность Е бумажного листа.
22) Как называется мощность оптического излучения, оцениваемая зрительным ощущением?
23) Какой спектр характерен для нагретых многоатомных разреженных газов?
24) Как называется отношение светового потока, падающего на некоторый участок поверхности, к площади этого участка?
25) Лампа, в которой светящим телом служит накаленный шарик диаметром d = 3 мм, дает силу света I = 85 кд. Найти яркость L лампы, если сферическая колба лампы сделана из прозрачного стекла. Диаметр колбы D = 6 см.
Ответы на модуль 9 (ВОЛНОВАЯ ОПТИКА) по предмету физика.
1) Что называется дифракцией?
совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики
радиус m-го темного кольца Ньютона
3) Как называется явление пространственного перераспределения энергии излучения при наложении двух или нескольких световых волн?
4) Каково условие дополнительного минимума для дифракционной решетки?
5) Найти наибольший порядок k спектра для желтой линии натрия (λ = 589 нм), если постоянная дифракционной решетки d = 2 мкм.
6) На щель шириной а = 6λ падает нормально параллельный пучок монохроматического света с длиной волны λ. Под каким углом φ будет наблюдаться третий дифракционный минимум света?
7) Как называется дифракция плоских световых волн или дифракция в параллельных лучах, когда размер отверстия меньше размера зоны Френеля?
радиус m-го светлого кольца Ньютона
9) Как называется дифракция сферических световых волн или дифракция в сходящихся лучах, когда размер отверстия сравним с размером зоны Френеля?
10) Выберите формулу для расчета степени поляризации света.
12) Каковы условия максимума и минимума для разности хода двух световых лучей?
14) На мыльную пленку падает белый свет под углом I = 45° к поверхности пленки. При какой наименьшей толщине пленки отраженные лучи будут окрашены в желтый цвет (λ = 600 нм)? Показатель преломления мыльной воды n = 1,33.
15) На дифракционную решетку нормально падает пучок света от разрядной трубки, наполненной гелием. На какую линию в спектре третьего порядка накладывается красная линия гелия спектра второго порядка?
16) Найти угол полной поляризации при отражении света от стекла, показатель преломления которого n = 1,57.
17) На дифракционную решетку падает нормально пучок света. Для того чтобы увидеть красную линию (λ = 700 нм) в спектре этого порядка, зрительную трубку пришлось установить под углом φ = 30° к оси коллиматора. Найти постоянную дифракционной решетки.
18) Как называется различное поглощение света в зависимости от ориентации электрического вектора световой волны?
19) При освещении кварцевого клина монохроматическими лучами (λ = 600 нм), перпендикулярными к его поверхности, наблюдаются в отраженном свете интерференционные полосы, ширина которых 8,1 мм. Показатель преломления кварца 1,54. Определить преломляющий угол клина.
21) Какова степень поляризации естественного света?
22) Какой свет называется поляризованным?
свет, в котором направления колебаний светового вектора каким-то образом упорядочены
23) Как называется явление возникновения двух ортогональных линейно поляризованных составляющих оптического излучения при распространении в оптически анизотропной среде?
24) Какой свет называется плоскополяризованным?
свет, в котором вектор колеблется только в одном направлении, перпендикулярном лучу
25) Какая из приведенных ниже формул выражает закон Малюса?
Ответы на модуль 10 (КВАНТОВАЯ ФИЗИКА) по предмету физика.
1) Каков физический смысл волновой функции?
определяет вероятность нахождения микрочастицы в фиксированный момент времени в малой области пространства
2) Выберите формулу для расчета энергии Ферми.
3) Укажите 3-й постулат Бора.
переход электрона с одной стационарной орбиты на другую сопровождается излучением или поглощением атомом кванта энергии; квант энергии, на основании закона сохранения энергии, равен разности энергий стационарных состояний атома до и после излучения
4) Укажите соотношение неопределенностей Гейзенберга.
5) Выберите формулу для расчета кинетической энергии квантовой частицы в «потенциальной яме».
6) Какой функцией описывается состояние частицы в случае нестационарного трехмерного потенциального поля?
8) Укажите уравнение Эйнштейна для внешнего фотоэффекта.
9) Найти температуру Т печи, если известно, что излучение из отверстия в ней площадью имеет мощность N = 34,6 Вт. Излучение считать близким к излучению абсолютно черного тела.
10) Укажите 1-й постулат Бора.
электроны в атоме могут вращаться вокруг ядра не по любым, а только по разрешенным орбитам, вполне определенного радиуса, определяемого для атома водорода по формуле
11) Фотоэлемент с наибольшей избирательной чувствительностью в ближней инфракрасной области облучается монохроматическим светом с длиной волны 486 нм. Определить наибольшую скорость фотоэлектронов, если работа выхода из материала фотокатода равна 1,56 эВ.
12) Какая из приведенных ниже формул выражает закон Стефана-Больцмана?
13) Каким соотношением связана величина момента импульса с орбитальным, квантовым числом?
14) Найти массу m фотона, если соответствующая ему длина волны λ = 1,6 пм.
15) Из трех законов внешнего фотоэффекта выберите закон Столетова.
при фиксированной частоте падающего света число фотоэлектронов, вырываемых из катода в единицу времени, пропорционально световому потоку
16) Найти задерживающую разность потенциалов U для электронов, вырываемых при освещении калия светом с длиной волны λ = 330 нм.
17) С какой скоростью v должен двигаться электрон, чтобы его импульс был равен импульсу фотона с длиной волны λ = 520 нм?
18) Какую энергетическую светимость имеет абсолютно черное тело, если максимум спектральной плотности его энергетической светимости приходится на длину волны λ = 484 нм?
19) Как называется тело, которое полностью поглощает все падающее на него электромагнитное излучение?
абсолютно черное тело
20) При нагревании абсолютно черного тела длина волн λ, на которую приходится максимум спектральной плотности энергетической светимости, изменилась от 690 до 500 нм. Во сколько раз увеличилась при этом энергетическая светимость?
21) Укажите 2-й постулат Бора.
электрон на каждой орбите обладает определенной энергией; такие орбиты называются стационарными; движение электронов по стационарным орбитам не сопровождается излучением или поглощением энергии атомом
22) Укажите уравнение Э. Шредингера для стационарного трехмерного потенциального поля.
23) Найти наибольшую длину волны λ в ультрафиолетовой области спектра водорода.
24) Найти радиус первой боровской электронной орбиты для однократно ионизированного гелия.
25) Укажите уравнение Э. Шредингера для частицы, находящейся в «потенциальной яме».
Ответы на модуль 11 (ФИЗИКА АТОМНОГО ЯДРА) по предмету физика.
4) Какая температура необходима для протекания термоядерных реакций?
6) Из каких элементарных частиц состоит атомное ядро?
протонов и нейтронов
8) При бомбардировке изотопа лития дейтронами (ядрами дейтерия ) образуются две α-частицы. При этом выделяется энергия Q = 22,3 МэВ. Зная массы дейтрона и α-частицы, найти массу m изотопа лития
9) Какой изотоп образуется из после трех α-распадов и двух β-распадов?
10) Сколько атомов радона распадается за время Δt = 1 сут из атомов?
11) Найти постоянную распада λ радона, если известно, что число атомов радона уменьшается за время Δt = 1 сут на 18%.
12) Укажите размеры атомных ядер.
13) Как называются ядра с одинаковыми атомными номерами Z, но разными массовыми числами А?
15) Какая из приведенных ниже формул выражает энергию связи нуклонов в ядре?
16) Какая из приведенных ниже формул определяет закон радиоактивного распада?
17) Как называются ядра с одинаковыми массовыми числами А, но разными атомными номерами Z?
18) Как называется самопроизвольное превращение одних атомных ядер в другие, сопровождаемое испусканием элементарных частиц?
19) Из какой наименьшей массы m руды, содержащей 42% чистого урана, можно получить массу радия?
22) Выберите формулу для расчета периода полураспада радиоактивного ядра.
24) Какая из приведенных размерностей соответствует активности радиоактивного вещества?